Глава IX. Иные разрешающие процедуры.
- Дизъюнктивно и конъюнктивно нормальные формы
Нормальные формулы, или точнее, конъюнктивно и дизъюнктивно нормальные формы суть еще одна разрешающая процедура, применяемая в логике высказываний для определения тождественно-истинных и тождественно-ложных формул. Способ, о котором пойдет речь ниже, является альтернативным построению таблиц истинности. Он более сложный, но необычайно важный с точки зрения наработки студентами навыков для оперирования логическими эквивалентностями.
Прежде, чем перейти к нормальным формам логики высказываний, необходимо оговориться: в логике, в следствие эквивалентных преобразований, существует много разных языков, которые не используют всего массива логических знаков. Иными словами, есть языки, которые используют лишь конъюнкцию и импликацию, игнорируя дизъюнкцию; есть языки, которые используют импликацию и дизъюнкцию, игнорируя знаки конъюнкции. Есть языки, которые не используют знак импликации и оперируют только конъюнкцией и дизъюнкцией.
Здесь, вероятно, нужны примеры.
Известные логики и математики Д. Гильберт и В. Аккерман предпочитают систему, в которой не существует знака дизъюнкции. Для них формула «A˅B˄C⊃D» будет выглядеть так: «AB&C→D». Для большинства современных логиков та же самая формула «A˅B˄C⊃D» может быть написана как «A˅BC→D». Нам же нужно переписать эту формулу не используя знака импликации.
Формула должна представлять собой последовательность элементарных конъюнкций, соединённых знаками дизъюнкции (нормальная дизъюнктивная форма), либо последовательность элементарных дизъюнкций, соединённых знаками конъюнкции (нормальная конъюнктивная форма).
Иными словами, нормальная дизъюнктивная форма представляет собой последовательность вида «(a˄b)˅(c˄d)˅(e˄f)…», а нормальная конъюнктивная форма – последовательность вида «(a˅b)˄(c˅d)˄(e˅f)…»
Когда нормальная форма формулы будет построена, можно будет легко определить – является ли она тождественно-ложной или тождественно-истинной.
Если формула принимает значение конъюнктивно нормальной формы, где все ее дизъюнкции содержат переменную и, одновременное, ее отрицание, значит формула – тождественно-истинная. Например: «(a˅¬a)˄(b˅¬b)˄(c˅¬c)…» Если же дизъюнктивно нормальная форму формулы содержит противоречие в каждой конъюнкции, то формула – тождественно-ложная. Например: «(a˄¬a)˅(b˄¬b)˅(c˄¬c)…» Соответственно, если оба этих условия не выполняются, то формула, скорее всего, выполнима или опровержима.
Для начала необходимо объяснить алгоритм приведения формулы в нормальные формы.
- Путем применения логических эквивалентностей мы добиваемся, чтобы формула содержала лишь знаки конъюнкции, дизъюнкции и отрицания. Для этого мы используем эквивалентности –
a⊃b↔¬a˅b (или, что тоже самое «a⊃b↔¬(a˄¬b)») – для удаления импликации;
a≡b↔(¬a˅b)˄(a˅¬b) (или «a≡b↔(a∧b)∨(¬a˄¬b)») – для удаления тождества;
a˅b↔¬((a∨¬b)∧(¬a∨b)) – для удаления строгой дизъюнкции.
- Все отрицания, стоящие перед скобками, преобразуем в отрицания, стоящие непосредственно перед переменными. Для этого применяем законы де Моргана:
¬(a˅b)↔¬a˄¬b
¬(a˄b)↔¬a˅¬b
- 3. Устраняем все двойные отрицания.
- Раскрываем скобки, используя законы дистрибутивности:
a˄(b˅c)↔(a˄b)˅(а˄c) — дистрибутивность конъюнкции относительно дизъюнкции;
a˅(b˄c)↔(a˅b)˄(а˅c) — дистрибутивность дизъюнкции относительно конъюнкции;
- По необходимости, сокращаем формулу по законам –
a˄(a˅b)↔a – первый закон поглощения;
a˅(a˄b)↔a – второй закон поглощения;
a˄(b˅¬b)↔a – закон исключения истинного члена из конъюнкции;
a˅(b˄¬b)↔a – закон исключения ложного члена из дизъюнкции.
Для удобства, во время всего процесса применяем законы ассоциативности и коммутативности:
(a˄b)˄c↔a˄(b˄c) — ассоциативность конъюнкции;
(a˅b)˅c↔a˅(b˅c) – ассоциативность дизъюнкции;
(a˄b)↔(b˄a) – коммутативность конъюнкции;
(a˅b)↔(b˅а) – коммутативность дизъюнкции.
Для того чтобы понять данный алгоритм (который требует высокой сосредоточенности и творческого мастерства студента) попробуем решить какую-нибудь простую задачу. К приме, попробуем построить нормальные формы формулы контрапозиции: (p⊃q)⊃(¬q⊃¬p).
- Преобразуем импликации. Сначала главную импликацию выражения
(p⊃q)⊃(¬q⊃¬p)→¬(p⊃q)˅(¬q⊃¬p)
Затем преобразовываем остальные импликации:
¬(p⊃q)˅(¬q⊃¬p)→(p˄¬q)˅(¬¬q˅¬p)
Пояснение: импликацию «¬(p⊃q)» мы преобразили, по правилу отрицания импликации «¬(p⊃q)→(p˄¬q)», а импликацию «(¬q⊃¬p)» по эквивалентности «a⊃b↔¬a˅b».
- Второе действие алгоритма мы опускаем, поскольку у нас нет отрицаний, стоящих перед скобками.
- Устраняем двойные отрицания:
(p˄¬q)˅(¬¬q˅¬p)→(p˄¬q)˅(q˅¬p)
- Раскрываем скобки, используя законы дистрибутивности (для удобства меняем местами скобки по закону ассоциативности):
(p˄¬q)˅(q˅¬p)→(q˅¬p)˅(p˄¬q) — по закону ассоциативности;
(q˅¬p)˅(p˄¬q)→(q˅¬p˅p)˄(q˅¬p˅¬q) – по закону дистрибутивности дизъюнкции относительно конъюнкции.
Итак, нормальная конъюнктивная форма построена – «(q˅¬p˅p)˄(q˅¬p˅¬q)». Поскольку в каждой её дизъюнкции присутствует переменная и её отрицание, делаем вывод, что изначальная формула тождественно-истинная.
Попробуем построить нормальную форму тождественно-ложной формулы. Например, «¬(((a⊃b)˄a)⊃b)»
| ¬(((a⊃b)˄a)⊃b)→ | |
| →((a⊃b)˄a)˄¬b→ | (по правилу эквивалентности «¬(a⊃b)↔a˄¬b») |
| →(¬a˅b)˄a˄¬b→ | (по правилу эквивалентности «a⊃b↔¬a˅b») |
| →(a˄¬b)˄(¬a˅b)→ | (по правилу коммутативности конъюнкции «(a˄b)↔(b˄a)») |
| →(a˄¬b˄¬a)˅(a˄¬b˄b) | (по правилу дистрибутивности конъюнкции относительно дизъюнкции «a˄(b˅c)↔(a˄b)˅(а˄c)»). |
Нормальная дизъюнктивная форма «(a˄¬b˄¬a)˅(a˄¬b˄b)» соответствует всем признакам тождественно-ложной формулы, поскольку в каждом дизъюнкте присутствует противоречие.
Для закрепления навыков, попробуем решить какую-нибудь выполнимую формулу.
Предположим, дано умозаключение: «Чтобы приготовить вкусный борщ, в него обязательно надо добавить жареный лук и чеснок. А это означает, что для его приготовления нужна какая-нибудь готовая заправка».
Строим нормальную дизъюнктивную форму:
| (a⊃(b˅c))⊃(a⊃d)→
|
|
| →¬(a⊃(b˅c))˅(a⊃d)→ | (по правилу эквивалентности «a⊃b↔¬a˅b») |
| →¬(a⊃(b˅c))˅(¬a˅d)→ | (по правилу эквивалентности «a⊃b↔¬a˅b») (по правилу эквивалентности «¬(a⊃b)↔a˄¬b») |
| →¬(¬a˅(b˅c))˅(¬a˅d)→ | (по правилу эквивалентности «a⊃b↔¬a˅b») |
| →(¬¬a˄¬(b˅c))˅(¬a˅d)→ | (по закону Де Моргана (по отрицанию дизъюнкции) – «¬(a˅b)↔¬a˄¬b») |
| →(a˄¬(b˅c))˅(¬a˅d)→ | по закону удаления двойного отрицания |
| →(a˄¬b˄¬c)˅(¬a˅d) | (по закону Де Моргана (по отрицанию дизъюнкции) – «¬(a˅b)↔¬a˄¬b») |
По полученной дизъюнктивной форме «(a˄¬b˄¬c)˅(¬a˅d)» видно, что анализируемое умозаключение не является тождественно-ложным.
Строим нормальную конъюнктивную форму:
| (a⊃(b˅c))⊃(a⊃d)→
|
|
| →¬(a⊃(b˅c))˅(a⊃d)→ | (по правилу эквивалентности «a⊃b↔¬a˅b») |
| →¬(a⊃(b˅c))˅(¬a˅d)→ | (по правилу эквивалентности «a⊃b↔¬a˅b») (по правилу эквивалентности «¬(a⊃b)↔a˄¬b») |
| →¬(¬a˅(b˅c))˅(¬a˅d)→ | (по правилу эквивалентности «a⊃b↔¬a˅b») |
| →(¬¬a˄¬(b˅c))˅(¬a˅d)→ | (по закону Де Моргана (по отрицанию дизъюнкции) – «¬(a˅b)↔¬a˄¬b») |
| →(a˄¬(b˅c))˅(¬a˅d)→ | по закону удаления двойного отрицания |
| →(a˄¬b˄¬c)˅(¬a˅d)→ | (по закону Де Моргана (по отрицанию дизъюнкции) – «¬(a˅b)↔¬a˄¬b») |
| →(¬a˅d)˅(a˄¬b˄¬c)→ | (по правилу коммутативности дизъюнкции «(a˅b)↔(b˅а))» |
| →(¬a˅d˅a)˄(¬a˅d˅¬b)˄(¬a˅d˅¬c) | (по правилу дистрибутивности дизъюнкции относительно конъюнкции «a˅(b˄c)↔(a˅b)˄(а˅c)») |
По полученной конъюнктивной форме «(¬a˅d˅a)˄(¬a˅d˅¬b)˄(¬a˅d˅¬c)» видно, что анализируемое умозаключение не является тождественно-истинным. Следовательно, умозаключение формы «Чтобы приготовить вкусный борщ, в него обязательно надо добавить жареный лук и чеснок. А это означает, что для его приготовления нужна какая-нибудь готовая заправка» может быть истинным (или ложным) при определенных условиях.
Совет
| Если вам необходимо построить одновременно, как дизъюнктивно нормальную форму, так и конъюнктивно нормальную форму, начинайте своё построение, не задумываясь о том, какая именно форма у вас в результате получится. Получив одну из них, вы легко преобразуете в её другую, применив соответствующее правило дистрибутивности. |
- Аналитические таблицы
Если приведение формулы в нормальную форму является разрешающей процедурой только в логике высказываний, то очень популярный сегодня метод проверки формул путем построения аналитических таблиц является полуразрешающей процедурой также и для логики предикатов первого порядка.
При построении аналитических таблиц используется несколько иной язык логики (по сравнению с тем, с которым мы с вами до сих пор сталкивались). Формула «a» обозначается как ложная выражением «Fa» (от английского «false» — ложный) и, соответственно в качестве истинной она обозначается как «Ta» (от английского «truth» — истинный).
Поскольку каждая формула в аналитических таблицах позиционируется как некое множество, она берется в фигурные скобки – «{Fa}». Методом построения аналитических таблиц всего служит метод от противного, т.е. изначально предполагается, что искомая формула ложна — «{Fa}». Затем, применяя к формуле определенные правила, мы пытаемся (как в случае с семантическими таблицами) «замкнуть» таблицу. Если нам это удается – искомая формула считается тождественно-истинной.
Правила, применяемые для аналитических таблиц, делятся на две группы – правила «истинности» и правила «ложности»:
| T˄ | {T(a˄b)} | F˄ | {F(a˄b)} | ||||||
| {Ta, Tb} | {Fa}, {Fb} |
| T˅ | {T(a˅b)} | F˅ | {F(a˅b)} | ||||||
| {Ta}, {Tb} | {Fa, Fb} |
| T⊃ | {T(a⊃b)} | F⊃ | {F(a⊃b)} | ||||||
| {Fa}, {Tb} | {Ta, Fb} |
| T¬ | {T¬a} | F¬ | {F¬a} | ||||||
| {Fa} | {Ta} |
Также существуют правила для кванторов:
| T∃ | {T∃xA(x)} | F∃ | {F∃xA(x)} | ||||||
| {TA(β)} | {F∃xA(x), FA(β)} |
| T∀ | {T∀xA(x)} | F∀ | {F∀xA(x)} | ||||||
| {T∀xA(x)}, TA(β)} | {FA(β)} |
Правила мы описали, теперь перейдем к практическому решению задач.
Предположим, дана формула «(a⊃b)⊃(¬a˅b)» — известная вам эквивалентность. Предполагаем, что она ложная, т.е «F»:
- {{F((a⊃b)⊃(¬a˅b))}}
Вывод из ложной импликации мы производим, соответственно, по правило «F⊃»: {F(a⊃b)}⊨{Ta, Fb}:
- {{T(a⊃b), F(¬a˅b)}} – из 1 по F⊃
- {{T(a⊃b), F¬a, Fb}} – из 2 по F˅
- {{T(a⊃b), Ta, Fb}} – из 3 по F¬
- {{Fa, Ta, Fb}, +{Tb, Ta, Fb}=} – из 4 по F⊃
Пояснение действия 5: По правилу F⊃ мы должны разбить множество {T(a⊃b), Ta, Fb} надвое. Из «T(a⊃b)» по правилу F⊃ получаем {Fa} и {Tb}. Но, поскольку в действии 4 у нас остаётся множество {Ta, Fb}, мы его помещаем, и в правое, и в левое множества последовательности формул. Иными словами {Fa}+{Ta, Fb}={Fa, Ta, Fb} и {Tb}+{Ta, Fb}={Tb, Ta, Fb}. Теперь мы видим противоречия в обоих множествах. В левом {Fa} и {Ta}, а в правом – {Tb} и {Fb}. Таким образом, исходная формула тождественно-истинная.
Доказываем закон дистрибутивности конъюнкции относительно дизъюнкции – «a˄(b˅c)⊃(a˄b)˅(а˄c)»:
| 1. {{F(a˄(b˅c)⊃(a˄b)˅(а˄c))}} | |
| 2. {{Т(a˄(b˅c)), F((a˄b)˅(а˄c))}} | F⊃ |
| 3. {{Ta, T(b˅c), F((a˄b)˅(а˄c))}} | T˄ |
| 4. {{Tb, Ta, F((a˄b)˅(а˄c))}, {Tc, Ta, F((a˄b)˅(а˄c))}} | T˅ |
| 5. {{Tb, Ta, F(a˄b), F(а˄c)}, {Tc, Ta, F(a˄b), F(а˄c)}} | F˅ |
| 6. {{Tb, Ta, Fa, F(а˄c)}, {Tb, Ta, Fb, F(а˄c)}, {Tc, Ta, Fa, F(а˄c)}, {Tc, Ta, Fb, F(а˄c)}} | F˄ |
| 7. {{Tb, Ta, Fa, Fа}, {Tb, Ta, Fc, Fа}, {Tb, Ta, Fb, Fа}, {Tb, Ta, Fb, Fc}, {Tc, Ta, Fa, Fа}, {Tc, Ta, Fa, Fc}, {Tc, Ta, Fb, Fа}, {Tc, Ta, Fb, Fc}} | F˄ |
Аналитическая таблица замкнулась – в каждом конечном множестве мы имеем противоречие (для наглядности мы подчеркнули их).
Поясним переход от третьего действия к четвертому. Мы его совершили по правилу
| T˅ | {T(a˅b)} |
| {Ta}, {Tb} |
Иными словами, нам было необходимо из одного множества перейти к двум. Соответственно, из «T(b˅c)» мы получили «Tb» и «Tc», которые необходимо распределить между двумя множествами: «Tb» слева и «Tc» справа:
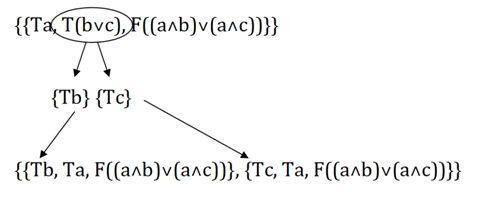
Более сложной задачей является построение аналитической таблицы для формулы логики предикатов, поскольку здесь добавляются правила для кванторов. К правилам кванторов необходимо добавить некоторые пояснения.
Для T∃ и F∀, «β» — новый параметр, который не встречался в предшествующих конфигурациях.
Для F∃ и T∀, «β» — любой параметр из уже имеющихся, либо новый параметр, если параметров ещё нет.
Например, «¬∀x(S(x))⊃∃x¬(S(x))».
| 1. {{F¬(∀x(S(x))⊃∃x¬(S(x)))}} | |
| 2. {{Т(¬∀x(S(x))), F(∃x¬(S(x)))}} | F⊃ |
| 3. {{F(∀x(S(x))), F(∃x¬(S(x))}} | T¬ |
| 4. {{FS(β), F(∃x¬(S(x))}} | F∀ |
| 5. {{FS(β), F(∃x¬(S(x)), F¬(S(β))}} | F∃ |
| 6. {{FS(β), F(∃x¬(S(x)), TS(β)}} | F¬ |
Таблица замкнулась.
Еще пример: «∃x∀y(S(x, y))⊃∀y∃x(S(x, y))».
| 1. {{F(∃x∀y(S(x, y))⊃∀y∃x(S(x, y)))}} | |
| 2. {{T(∃x∀y(S(x, y))), F(∀y∃x(S(x, y)))}} | F⊃ |
| 3. {{T∀y(S(β, y)), F(∀y∃x(S(x, y)))}} | T∃ |
| 4. {{T∀y(S(β, y)), F∃x(S(x, θ))}} | F∀ |
| 5. {{T∀y(S(β, y)), FS(β, θ), F∃x(S(x, γ))}} | F∃ |
| 6. {{T∀y(S(β, y)), TS(β, θ), FS(β, θ), F∃x(S(x, γ))}} | T∀ |
3. Аксиоматические исчисления
В рамках аксиоматической системы используются схемы аксиом (или аксиомы), причем их количество может быть сведено к минимуму:
- a⊃(b⊃a) – схема утверждения консеквента (и аксиомы, сформулированные на её основе);
- (a⊃(b⊃c))⊃((a⊃b)⊃(a⊃c)) – схема самодистрибутивности импликации (и аксиомы, сформулированные на её основе);
- (¬b⊃¬a)⊃(a⊃b) – схема обратной контрапозиции.
Добавляется лишь одно правило – Modus Ponens
| M.P. | a⊃b, a |
| b |
Для работы с языком логики предикатов первого порядка, формулируются схемы аксиом для кванторов:
- ∀xP(x) ⊧P(t) – схема удаления ∀ (У∀)
- P(t) ⊧ƎхP(x) – схема введения Ǝ (ВƎ)
- ∀x(А⊃P(x))⊧(А⊃∀xP(х)) – схема введения ∀ в консеквент (В∀вК).
- ∀x(P(x)⊃А)⊧(ƎхP(х)⊃А) – схема введения Ǝ в антецедент (ВƎвА).
А также правило «P(t)⊧∀xP(x)» — правило обобщения (В∀)
Докажем аксиому «¬(a˄a)→¬a».
Для начала, преобразуем формулу путем логических эквивалентностей – «(a⊃¬a)⊃¬a»
- a⊃(a⊃¬a)⊃¬a – аксиома, построенная на основе схемы утверждения консеквента.
- 2. (a⊃(a⊃¬a)⊃¬a)⊃(((a⊃¬a)⊃(a⊃a))⊃((a⊃¬a)⊃¬a))) — аксиома, построенная на основе схемы самодистрибутивности материальной импликации.
- ((a⊃¬a)⊃(a⊃a))⊃((a⊃¬a)⊃¬a)) – из 1 и 2 по Modus Ponens.
- (a⊃¬a)⊃(a⊃a) — аксиома, построенная на основе схемы утверждения консеквента.
- (a⊃¬a)⊃¬a – из 3 и 4 по Modus Ponens. ∎
С помощью системы аксиоматического вывода можно доказать любую тождественно-истинную формулу. И (если мы говорим о логике высказываний) в выводе неизменно будет сохраняться указанные пять действий (т.е. выше представлена «схема» доказательства). К безусловным преимуществам аксиоматического вывода можно отнести минимальное количество правил и схем аксиом. К неудобствам – поиск аксиом из правил консеквента и самодистрибутивности импликации, а также крайне длинные формулы, изобилующие множеством скобок. В приведенном примере мы доказывали формулу с одной пропозициональной переменной. Если бы переменных в формуле было бы четыре или пять, вывод мог бы растянуться на несколько страниц. Такое, прямо скажем, не самое изящное доказательство является «расплатой» за минимальное количество схем вывода.
Добавив к перечисленным схемам вывода всего одну схему, схему исключения конъюнкции– «ab⊃a», где написание «ab» есть сокращение от «a˄b», мы сможем доказывать формулы значительно компактнее.
Доказательство формулы «a⊃(b⊃c)⊨ab⊃c»:
- + a⊃(b⊃c) – гипотеза.
- (ab⊃(b⊃c))⊃((ab⊃b)⊃(ab⊃c)) – схема самодистрибутивности импликации;
- (ab⊃(a⊃(b⊃c)))⊃((ab⊃a)⊃(ab⊃(b⊃c))) – схема на основе самодистрибутивности импликации;
- (a⊃(b⊃c))⊃(ab⊃(a⊃(b⊃c))) – схема на основе утверждения консеквента;
- ab⊃(a⊃(b⊃c)) – из 4 и 1 по Modus Ponens;
- (ab⊃a)⊃(ab⊃(b⊃c)) – из 5 и 3 по Modus Ponens;
- ab⊃a – схема исключения конъюнкции;
- ab⊃(b⊃c) – из 6 и 7 по Modus Ponens;
- (ab⊃b)⊃(ab⊃c) – из 2 и 8 по Modus Ponens;
- ab⊃b — схема исключения конъюнкции;
- ab⊃c – из 9 и 10 по Modus Ponens. ∎
Для облегчения работы в аксиоматической системе с языком логики предикатов можно взять из системы натурального вывода все правила первого и второго рода и интерпретировать их в качестве схем аксиом; однако вместо правил для кванторов рекомендуем использовать схемы аксиом для них:
- ∀xP(x) ⊧P(t) – (У∀);
- P(t) ⊧ƎхP(x) – (ВƎ);
- ∀x(А⊃P(x))⊧(А⊃∀xP(х)) – (В∀вК);
- ∀x(P(x)⊃А)⊧(ƎхP(х)⊃А) – (ВƎвА);
а также правило «P(t)⊧∀xP(x)» — (В∀).
Дано: «∀x(S(x)⊃P(x))⊃∃x(S(x)∧P(x))»
Решение:
- + ∀x(S(x)⊃P(x)) – гипотеза;
- + ∀xS(x) – гипотеза;
- S(x)⊃P(x) – из 1 по схеме У∀;
- S(x) – из 2 по схеме У∀;
- P(x) – из 3 и 4 по схеме У⊃;
- S(x)˄P(x) — из 4 и 5 по схеме В˄;
- ∃x(S(x)∧P(x)) – из 6 по схеме ВƎ. ∎
Студент должен понимать, что аксиоматическая система может иметь в своем арсенале различные схемы аксиом. Только что решенную задачу можно было бы решить в два действия, имея в виду, что среди заявленных систем аксиом имелась бы «∀x(S(β)⊃P(γ))⊃∃x(S(β)∧P(γ))».
Дано: «∀x(S(x)⊃P(x))⊃∃x(S(x)∧P(x))»
Решение:
- + ∀x(S(x)⊃P(x)) – гипотеза;
- ∃x(S(x)∧P(x)) из 1 по схеме аксиом ∀x(S(β)⊃P(γ))⊃∃x(S(β)∧P(γ)). ∎
Попробуем решить задачу.
Дано высказывание: «Если неправда, что некоторые студенты наркоманы, следовательно, верно, что все студенты не наркоманы».
Переводим высказывание в символическую форму:
¬(ƎхP(х))→∀x¬P(x)
- + ¬ ƎхP(х)
- + P(x)
- ƎхP(х) — из 2 по ВƎ
- ¬ ƎхP(х)˄ ƎхP(х) из 1 и 3 по В˄
- (¬ ƎхP(х)˄ ƎхP(х))→ P(x) из 4 и 2 по В→
- ¬ P(х) – из 5 по ДОП
- ∀x¬P(x) – из 6 по В∀вК
- ¬ (ƎхP(х))→∀x¬P(x) – из 1 и 7 по В→.∎
Можно эту же задачу решить, используя доказательство от противного:
- +¬(¬ ƎхP(х)→∀x¬P(x))
- ¬ ƎхP(х)˄¬∀x¬P(x) из 1 по О→
- ¬ ƎхP(х) – из 2 по У˄
- ¬∀x¬P(x) – из 2 по У˄
- ¬Ǝx¬P(x) из 4 по ВƎвА
- ¬ ƎхP(х)˄ ¬Ǝx¬P(x) из 3 и 5 по В˄
- (¬ ƎхP(х)˄ ¬Ǝx¬P(x))→ ¬(¬ ƎхP(х)→∀x¬P(x)) из 6 и 1 по В→
- ¬ ƎхP(х)→∀x¬P(x)) из 7 по ДОП. ∎
В этом разделе мы привели несколько примеров систем аксиом, для решения некоторых логических формул. Студент должен понимать, что набор аксиом может быть абсолютно любым: главное, чтобы они помогали решить конкретную поставленную задачу. Предлагаем студентам самим поэкспериментировать в этом направлении. Главное, чтобы все аксиомы были тщательно проверенными, т.е. гарантированно являлись тождественно-истинными формулами.
