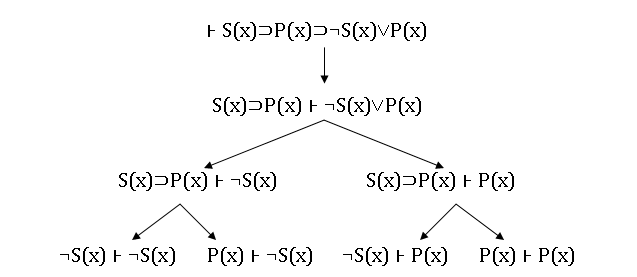Глава VIII. Исчисления секвенций.
Исчисление секвенций (от англ. Sequent calculus) — система формального вывода формул логики первого порядка предложенная немецким логиком Герхардом Генценом. Генценом были разработаны несколько эквивалентных вариантов исчисления секвенций.
Секвенциальные формулы представляют собой последовательность, разделенную знаком выводимости «⊦», в которой слева (в антецеденте) находится дизъюнктивная последовательность, а справа (в консеквенте, или в «сукцеденте») – конъюнктивная. В целом, секвенциальная формула выглядит следующим образом:
(a˅b˅c˅d˅…˅z) ⊦ (a˄b˄c˄d˄…˄z)
Подразумевается, что обе части уравнения эквивалентны в том смысле, что антецедент служит доказательством сукцедента, а сукцедент служит доказательством антецедента:
(a˅b˅c˅d˅…˅z) ↔ (a˄b˄c˄d˄…˄z)
Секвенция с пустым антецедентом интерпретируется как истина, а секвенция с пустым сукцедентом – как ложь. Если пустыми оказываются как антецедент, так и сукцедент — секвенция интерпретируется в качестве противоречивой:
∅ ⊦ (a˄b˄c˄d˄…˄z) – «истина»
(a˅b˅c˅d˅…˅z) ⊦ ∅ — «ложь»
∅ ⊦ ∅ — «противоречие»
Логические правила
| ˄L | Г, A ⊦ Δ | ˅R | Г ⊦ A, Δ | ||||||
| Г, A˄B ⊦ Δ | Г ⊦ A˅B, Δ |
| ˅L | Г, A ⊦ Δ | Σ, B ⊦ Π | ˄R | Г ⊦ A, Δ | Σ ⊦ B, Π | ||||||
| Г, Σ, A˅B ⊦ Δ, Π | Г, Σ ⊦ A˄B, Δ, Π |
| ⊃L | Г ⊦ A, Δ | Σ, B ⊦ Π | ⊃R | Г, A ⊦ B, Δ | ||||||
| Г, Σ, A⊃B ⊦ Δ, Π | Г ⊦ A⊃B, Δ |
| ¬L | Г ⊦ A, Δ | ¬R | Г, A ⊦ Δ | ||||||
| Г, ¬A ⊦ Δ | Г ⊦ ¬A, Δ |
| ∀L | Г, A[x/t] ⊦ Δ | ∀R | Г ⊦ A[x/y], Δ | ||||||
| Г, ∀tA ⊦ Δ | Г ⊦ ∀yA, Δ |
| ∃L | Г, A[x/y] ⊦ Δ | ∃R | Г ⊦ A[x/t], Δ | ||||||
| Г, ∃yA ⊦ Δ | Г ⊦ ∃tA, Δ |
где «t» — любая переменная (возможно «x», если «x» — свбодная переменная));
где «y» — любая новая переменная (либо уже имеющаяся перемененная «x», не связанная кванторами в Γ и ∆).
Эти две важнейшие оговорки мы объясним чуть позже на примерах.
Структурные правила:
| WL | Г ⊦ Δ | WR | Г ⊦ Δ | ||||||
| Г, A ⊦ Δ | Г ⊦ A, Δ |
| CL | Г, A, A ⊦ Δ | CR | Г ⊦ A, A, Δ | ||||||
| Г, A ⊦ Δ | Г ⊦ A, Δ |
| PL | Г1, A, B, Г2 ⊦ Δ | PR | Г ⊦ Δ1, A, B, Δ2 | ||||||
| Г1, B, A, Г2 ⊦ Δ | Г ⊦ Δ1, B, A, Δ2 |
| I (аксиома) | CUT (сечение) | Г ⊦ Δ, A | A, Σ ⊦ Π | |||||||
| A ⊦ A | Г, Σ ⊦ Δ, Π |
Символы «Г», «Δ», «Σ» и «Π» означают множества формул (возможно пустые).
Читатель, вероятно, уже обратил внимание, что правила исчисления секвенций не являются чем-то принципиально новым для нас. Все эти правила (в том или ином виде) мы встречали в системе натурального вывода.
Примеры вывода.
Пусть необходимо доказать аксиому «⊦ A⊃A».
Σ1. A ⊦ A – аксиома
Σ2. ⊦ A⊃A – из Σ1 по ⊃R ∎
Пусть необходимо доказать аксиому «⊦ A˅¬A».
| Σ1. A ⊦ A | I – аксиома |
| Σ2. ⊦ ¬A, A | из Σ1 по ¬R |
| Σ3. ⊦ A, ¬A | из Σ2 по PR |
| Σ4. ⊦ A, A˅¬A | из Σ3 по ˅R |
| Σ5. ⊦ A˅¬A | из Σ4 по CR ∎ |
Часто, для доказательства формулы необходимо наличие нескольких аксиом. Например, если мы доказываем формулу «A, B ⊦ A˄B», возможна следующая последовательность действий:
Σ1. A ⊦ A – аксиома
Σ2. B ⊦ B – аксиома
Σ3. A, B ⊦ A˄B – из Σ1 и Σ2 по ˄R ∎
Студент должен знать, что помимо линейного способа доказательства можно использовать табличный способ, отличающийся некоторыми эстетическими особенностями. Так, в табличной форме последнее доказательство выглядело бы так:
| A ⊦ A (I) | B ⊦ B (I) | ˄R |
| A, B ⊦ A˄B | ||
Табличная форма исчислений более распространена в практике исчисления секвенций, однако, она крайне неудобна для изложения в книжной полиграфии (по определенным техническим причинам).
Доказательство формулы «(A⊃(B˅C))⊃(((B⊃¬A)˄¬C)⊃¬A)» табличным способом:
| B ⊦ B | — I | C ⊦ C | — I | |||
| B˅C ⊦ B, C | — ˅L | |||||
| B˅C ⊦ C, B | — PR | |||||
| B˅C, ¬C ⊦ B | — ¬L | ¬A ⊦ ¬A | — I | |||
| (B˅C), ¬C, (B⊃¬A) ⊦ ¬A | — ⊃L | |||||
| (B˅C), ¬C, ((B⊃¬A)˄¬C) ⊦ ¬A | — ˄L | |||||
| (B˅C), ((B⊃¬A)˄¬C), ¬C ⊦ ¬A | — PL | |||||
| A ⊦ A | — I | (B˅C), ((B⊃¬A)˄¬C), ((B⊃¬A)˄¬C) ⊦ ¬A | — ˄L | |||
| ⊦ ¬A, A | — ¬R | (B˅C), ((B⊃¬A)˄¬C) ⊦ ¬A | — CL | |||
| ⊦ A, ¬A | — PR | ((B⊃¬A)˄¬C), (B˅C) ⊦ ¬A | — PL | |||
| ((B⊃¬A)˄¬C), (A⊃(B˅C)) ⊦ ¬A, ¬A | — ⊃L | |||||
| ((B⊃¬A)˄¬C), (A⊃(B˅C)) ⊦ ¬A | — CR | |||||
| (A⊃(B˅C)), ((B⊃¬A)˄¬C) ⊦ ¬A | — PL | |||||
| (A⊃(B˅C)) ⊦ (((B⊃¬A)˄¬C)⊃¬A) | — ⊃R | |||||
| ⊦ (A⊃(B˅C))⊃(((B⊃¬A)˄¬C)⊃¬A) | — ⊃R | |||||
Доказательство формулы «(A⊃(B˅C))⊃(((B⊃¬A)˄¬C)⊃¬A)» линейным способом:
Σ1. A ⊦ A – аксиома
Σ2. C ⊦ C — аксиома
Σ3. B˅C ⊦ B, C – из Σ1 и Σ2 по ˅L
Σ4. B˅C ⊦ C, B из Σ3 по PR
Σ5. B˅C, ¬C ⊦ B из Σ4 по ¬L
Σ6. ¬A ⊦ ¬A — аксиома
Σ7. (B˅C), ¬C, (B⊃¬A) ⊦ ¬A — из Σ5 и Σ6 по ⊃L
Σ8. (B˅C), ¬C, ((B⊃¬A)˄¬C) ⊦ ¬A – из Σ7 по ˄L
Σ9. (B˅C), ((B⊃¬A)˄¬C), ¬C ⊦ ¬A — из Σ8 по PL
Σ10. (B˅C), ((B⊃¬A)˄¬C), ((B⊃¬A)˄¬C) ⊦ ¬A- из Σ9 по ˄L
Σ11. (B˅C), ((B⊃¬A)˄¬C) ⊦ ¬A — из Σ10 по CL
Σ12. ((B⊃¬A)˄¬C), (B˅C) ⊦ ¬A — из Σ11 по PL
Σ13. ⊦ ¬A, A — из Σ1 по ¬R
Σ14. ⊦ A, ¬A — из Σ13 по PR
Σ15. ((B⊃¬A)˄¬C), (A⊃(B˅C)) ⊦ ¬A, ¬A — из Σ14 и Σ12 по ⊃L
Σ16. ((B⊃¬A)˄¬C), (A⊃(B˅C)) ⊦ ¬A — из Σ15 по CR
Σ17. (A⊃(B˅C)), ((B⊃¬A)˄¬C) ⊦ ¬A — из Σ16 по PL
Σ18. (A⊃(B˅C)) ⊦ (((B⊃¬A)˄¬C)⊃¬A) — из Σ17 по ⊃R
Σ19. ⊦ (A⊃(B˅C))⊃(((B⊃¬A)˄¬C)⊃¬A) — из Σ18 по ⊃R ∎
Мы специально привели достаточно сложный и длинный пример исчисления секвенций, чтобы использовать максимально большое количество правил. Разобрав каждый вывод, для студента в дальнейшем не будет сложностей с исчислением секвенций.
Но для классической логики работа с секвенциями связана также с использование правил кванторов. Для начала разберем незамысловатую задачу.
Пусть необходимо доказать формулу
«Ǝy(∀x(p(x, y))) ⊦ ∀x(Ǝy(p, (x, y)))»
| Σ1. p(x, y) ⊦ p(x, y) | I – аксиома |
| Σ2. ∀x(p(x, y)) ⊦ p(x, y) | из Σ1 по ∀L |
| Σ3. ∀x(p(x, y)) ⊦ ∃x(p(x, y)) | из Σ2 по ∃R |
| Σ4. ∃y(∀x(p(x, y))) ⊦ ∃x(p(x, y)) | из Σ3 по ∃L |
| Σ5. Ǝy(∀x(p(x, y))) ⊦ ∀x(Ǝy(p, (x, y))) | из Σ4 по ∀R ∎ |
Напомним, что для правил кванторов есть определенные ограничения (как и во всех остальных системах исчислений). Если для правил ∀L и ∃R ограничения несущественны, то для правил ∀R и ∃L следует помнить: получаемая переменная не должна быть связана в предыдущих выводах кванторами.
Предположим, мы хотим построить доказательство формулы вида «∃xP(x) ⊦ ∃xP(x)». Интуитивно мы понимаем, что какие бы кванторы не находились в антецеденте и сукцеденте формулы, ошибочным может быть только один вариант — «∃xP(x) ⊦ ∀xP(x)».
Начинаем, как обычно, с аксиомы:
Σ1. P(x) ⊦ P(x) – аксиома
Σ2. P(x) ⊦ ∃xP(x) – из Σ1 по ∃R
Σ3. ∃xP(x) ⊦ ∃xP(x) – из Σ2 по ∃L
Вывод построен неверно, поскольку правило ∃L в третьем действии нарушено: мы использовали переменную «x», которая уже была связана квантором общности во втором действии. Третье действие мы могли бы завершить только так:
Σ1. P(x) ⊦ P(x) – аксиома
Σ2. P(x) ⊦ ∃xP(x) – из Σ1 по ∃R
Σ3. ∀xP(x) ⊦ ∃xP(x) – из Σ2 по ∀L
В целом, у нас получилась правильная формула, однако мы так и не доказали искомую — «∃xP(x) ⊦ ∃xP(x)». Может быть наша ошибка заключалась в том, что мы начали не с той стороны? Попробуем еще раз:
Σ1. P(x) ⊦ P(x) – аксиома
Σ2. ∃xP(x) ⊦ P(x) – из Σ1 по ∃L
Σ3. ∃xP(x) ⊦ ∃xP(x) – из Σ2 по ∃R
Теперь правила выполнены.
Совет
| Соответственно, делаем для себя важный вывод: в исчислениях секвенций последовательность действий имеет значение. Сначала надо стараться использовать правила ∀R и ∃L, пока переменные не связаны кванторами. И лишь затем правила ∀L и ∃R. |
Вероятнее всего, последовательность действий будет важна и для решения формулы «∃xP(x) ⊦ ∃xP(x)»:
Σ1. P(x) ⊦ P(x) – аксиома
Σ2. ∀xP(x) ⊦ P(x) – из Σ1 по ∀L
Σ3. ∀xP(x) ⊦ ∀xP(x) – из Σ2 по ∀R
Вывод Σ3 сделан с нарушением правила ∀R. Пробуем в другой последовательности:
Σ1. P(x) ⊦ P(x) – аксиома
Σ2. P(x) ⊦ ∀xP(x) – из Σ1 по ∀R
Σ3. ∀xP(x) ⊦ ∀xP(x) – из Σ2 по ∀L
Теперь всё верно.
Попробуем усложнить задачу и доказать закон отрицания общеутвердительного суждения «¬∀xP(x) ⊦ ∃x¬P(x)»:
Σ1. ¬P(x) ⊦ ¬P(x) – аксиома
Σ2. ⊦ P(x), ¬P(x)– из Σ1 по ¬R
Σ3. ⊦ ∀xP(x), ¬P(x)– из Σ2 по ∀R
Σ4. ¬∀xP(x) ⊦ ¬P(x)– из Σ3 по ¬L
Σ5. ¬∀xP(x) ⊦ ∃x¬P(x)– из Σ4 по ∃R ∎
Теперь попробуем доказать формулу, записанную в расширенном виде «⊦ ∃x(S(x)˄¬P(x))⊃¬∀x(S(x)⊃P(x))».
Поскольку у нас два предиката, начнём построение секвенций с двух аксиом:
Σ1. S(x) ⊦ S(x) – аксиома
Σ2. P(x) ⊦ P(x) – аксиома
Мы должны получить импликацию, следовательно, преминяем закон ⊃L:
Σ3. S(x), S(x)⊃P(x) ⊦ P(x) – из Σ1 и Σ2 по ⊃L
Теперь надо получит конъюнкцию. Проще всего это сделать, прибавив произвольный термин в антецеденте формулы:
Σ4. S(x)˄¬P(x), S(x)⊃P(x) ⊦ P(x) – из Σ3 по ˄L
Перенеся из сукцедента в антецедент формулу «P(x)», получим повторение формулы «¬P(x)». Повторение убираем по правилу CL:
Σ5. S(x)˄¬P(x), ¬P(x), S(x)⊃P(x) ⊦ – из Σ4 по ¬L
Σ6. S(x)˄¬P(x), S(x)⊃P(x) ⊦ – из Σ5 по CL
Далее, вводим кванторы:
Σ7. ∃x(S(x)˄¬P(x)), S(x)⊃P(x) ⊦ – из Σ6 по ∃L
Σ8. ∃x(S(x)˄¬P(x)), ∀x(S(x)⊃P(x)) ⊦ – из Σ7 по ∀L
И, наконец, переносим формулу «∀x(S(x)⊃P(x))» из антецедента в сукцедент с отрицанием по правилу ¬R:
Σ9. ∃x(S(x)˄¬P(x)) ⊦ ¬∀x(S(x)⊃P(x))– из Σ8 по ¬R
Σ10. ⊦ ∃x(S(x)˄¬P(x))⊃¬∀x(S(x)⊃P(x))– из Σ9 по ⊃R ∎
Последнее действие совершено по правилу «⊃R», напоминающему правило дедукции.
Последнее исчисление представим в табличной форме:
| S(x) ⊦ S(x) – (I) | P(x) ⊦ P(x) – (I) | |
| S(x), S(x)⊃P(x) ⊦ P(x) | ⊃L | |
| S(x)˄¬P(x), S(x)⊃P(x) ⊦ P(x) | ˄L | |
| S(x)˄¬P(x), ¬P(x), S(x)⊃P(x) ⊦ | ¬L | |
| S(x)˄¬P(x), S(x)⊃P(x) ⊦ | CL | |
| ∃x(S(x)˄¬P(x)), S(x)⊃P(x) ⊦ | ∃L | |
| ∃x(S(x)˄¬P(x)), ∀x(S(x)⊃P(x)) ⊦ | ∀L | |
| ∃x(S(x)˄¬P(x)) ⊦ ¬∀x(S(x)⊃P(x)) | ¬R | |
| ⊦ ∃x(S(x)˄¬P(x))⊃¬∀x(S(x)⊃P(x)) | ⊃R | |
Как и в натуральной системе исчислений, в исчислении секвенций целесообразно применять дополнительные правила. Ими могут служить доказанные аксиомы и эквивалентности, известные законы логики, правила, используемые в аксиоматических системах и системе натурального вывода.
Например, правило Modus Ponens (иногда именуемое как «правило исключения импликации»)
| Г ⊦ A⊃B, Г ⊦ A | |
| Г ⊦ B |
К этому правилу можно добавить
| Сведение к абсурду | Г ⊦ A, Г ⊦ ¬A |
| Г ⊦ |
| Доказательство от противного | Г, ¬A ⊦ |
| Г ⊦ A |
| Введение конъюнкции | Г ⊦ A, Г ⊦ B |
| Г ⊦ A˄B |
| Удаление конъюнкции | Г ⊦ A˄B |
| Г ⊦ A |
| Правило удаления импликации | Г, ⊦ A⊃B |
| Г, A ⊦ B |
| Правило контрапозиции | Г, A ⊦ B |
| Г, ¬B ⊦ ¬A |
и так далее.
Используя дополнительные правила (например правило сведения к абсурду), некоторые задачи можно решить короче. Например, выводимость «⊦∀x(S(x)⊃P(x))⊃∀x(¬S(x)˅P(x))»:
Σ1. S(x)⊃P(x) ⊦ S(x)⊃P(x) – аксиома
Σ2. S(x)⊃P(x), S(x) ⊦ P(x) из Σ1 по правилу удаления импликации
Σ3. S(x)⊃P(x), S(x) ⊦ ¬S(x)˅P(x) из Σ2 по ˅R
Σ4. S(x)⊃P(x) ⊦ ¬S(x)˅P(x), ¬S(x) из Σ3 по ¬R
Σ5. S(x)⊃P(x), ¬(¬S(x)˅P(x)), ⊦¬S(x) из Σ4 по ¬R
Σ6. S(x)⊃P(x), ¬(¬S(x)˅P(x)), ⊦¬S(x)˅P(x) из Σ5 по ˅R
Σ7. ¬(¬S(x)˅P(x)) ⊦ ¬(¬S(x)˅P(x)) — аксиома
Σ8. S(x)⊃P(x), ¬(¬S(x)˅P(x)) ⊦ — из Σ6 и Σ7 по правилу сведения к абсурду
Σ9. S(x)⊃P(x) ⊦ ¬S(x)˅P(x) — из Σ8 по ¬R
Σ10. S(x)⊃P(x) ⊦ ∀x(¬S(x)˅P(x)) — из Σ9 по ∀R
Σ11. ∀x(S(x)⊃P(x)) ⊦ ∀x(¬S(x)˅P(x)) — из Σ10 по ∀L
Σ12. ⊦∀x(S(x)⊃P(x))⊃∀x(¬S(x)˅P(x)) — из Σ11 по правилу дедукции∎
Обращаем внимание на то, что в решении данной формулу мы применили два новых правила: правило удаления импликации (в действии 2) и правило сведения к абсурду (действие 8).
Понятно, что любая секвенция может иметь несколько решений. Например, формулу «⊦∀x(S(x)⊃P(x))⊃∀x(¬S(x)˅P(x))» можно решить по-другому:
Σ1. S(x)⊃P(x) ⊦ S(x)⊃P(x) – аксиома
Σ2. S(x)⊃P(x), S(x) ⊦ P(x) из Σ1 по правилу удаления импликации
Σ3. S(x)⊃P(x) ⊦ P(x), ¬S(x) из Σ2 по ¬R
Σ4. S(x)⊃P(x) ⊦ P(x), ¬S(x)˅P(x) из Σ3 по ˅R
Σ5. S(x)⊃P(x) ⊦ ¬S(x)˅P(x), ¬S(x)˅P(x) из Σ4 по ˅R
Σ6. S(x)⊃P(x) ⊦ ¬S(x)˅P(x) из Σ5 по CR
Σ7. S(x)⊃P(x) ⊦ ∀x(¬S(x)˅P(x)) — из Σ6 по ∀R
Σ8. ∀x(S(x)⊃P(x)) ⊦ ∀x(¬S(x)˅P(x)) — из Σ7 по ∀L
Σ9. ⊦∀x(S(x)⊃P(x))⊃∀x(¬S(x)˅P(x)) — из Σ8 по правилу дедукции∎
В качестве альтернативы построению семантических и аналитических таблиц, секвенциальные исчисления могут использоваться для построения «деревьев» в логике высказываний. Все правила остаются теми же, но доказательство ведется не из аксиом, а из самой доказываемой формулы.
Решаем последнюю формулу, опустив кванторы. Пусть дано «⊦ S(x)⊃P(x)⊃¬S(x)˅P(x)».
Найдя в формуле знак основной импликации, мы перестраиваем формулу в «S(x)⊃P(x) ⊦ ¬S(x)˅P(x)».
Поскольку в формуле есть дизъюнкция, значит, у нас появляется альтернатива: либо «S(x)⊃P(x) ⊦ ¬S(x)», либо «S(x)⊃P(x) ⊦ P(x)».
Теперь необходимо каким-то образом «разбить» импликацию. Преобразуем «S(x)⊃P(x)» в «¬S(x)˅P(x)». Таким образом, получаем еще две альтернативы: «¬S(x) ⊦ ¬S(x)», «P(x) ⊦ ¬S(x)» и «¬S(x) ⊦ P(x)», «P(x) ⊦ P(x)». Поскольку в последних альтернативах мы наблюдаем аксиомы, следовательно, искомая формула верная.