Индуктивные и правдоподобные умозаключения.
Считается, что дедукция – это нисхождение от общего к частному, а индукция – восхождения от частного к общему. Соответственно, дедуктивные умозаключения должны быть гарантированно истинными (необходимо истинными) , а индуктивные – лишь правдоподобными (вероятно истинными). В этом плане Шерлок Холмс был не прав, говоря, что его метод — дедуктивный. Великий сыщик собирал частные факты для построения общей картины преступления. Метод Шерлока Холмса – типичный случай индуктивного метода.
Но современная логика говорит, что гарантированно истинными могут быть как дедуктивные, так и индуктивные умозаключения. Поэтому понятия «индуктивные умозаключения» и «правдоподобные умозаключения» — не синонимы.
Мы уже убедились с вами на предыдущем материале, что истинными могут быть и недедуктивные выводы. Например, некоторые непосредственные выводы в простых суждениях или некоторые выводы в силлогистике. Правдоподобными же могут быть и не явно индуктивные умозаключения, как это мы наблюдали в модальной логике.
- Обратная дедукция.
Обратная дедукция означает, что, если из А с необходимостью следует B, то из B правдоподобно следует A.
Если дедуктивное следование мы обозначали символом «⊧ », то индуктивное следование мы будем обозначать символом «⊫».
Значит, если A⊧B, то B⊫A. Читаем: Если из A следует B, то из B правдоподобно (возможно) следует A: «B⊧◊A»
| A⊃B, B |
| ◊A |
Таким образом, неправильные модусы в системе дедуктивной логики могут быть правдоподобными в системе индуктивной логики. Скажем, Modus Ponens (неправильный):
| A⊃B, B |
| A |
в индуктивной логике является правильным с оговоркой «◊»:
| A⊃B, B |
| ◊A |
Если в силлогизмах вывод является необходимым, то в обратной дедукции мы получаем правдоподобные (вероятные) выводы.
Силлогизм
| Все философы – люди
Люди – грешны |
| Все философы – грешны |
можно перестроить в выражение обратной индукции:
|
Все философы – грешны |
| Правдоподобно, что все философы – люди, а люди – грешные |
А непосредственное умозаключение
|
Все философы знают логику |
| Некоторые философы знают логику |
можно представить в качестве вероятностного умозаключения
|
Некоторые философы знают логику |
| Вероятно, все философы знают логику |
Возникает вопрос: насколько эти выводы правдоподобны? Весьма правдоподобны или мало правдоподобны? Весьма вероятны или слабо вероятны?
Вероятность события вычисляется очень легко: это соотношение желаемого события к возможному. Например, бросая монету, вы хотите понять, какова вероятность того, что у вас выпадет «решка». Желаемое событие равно 1, возможных вариантов – 2. Значит, вероятность составляет ½.
Если вы кидаете игральную кость, надеясь на результат 6, вероятность этого составит уже 1/6. Если вы случайным образом надеетесь вытащить из колоды карт в 36 листов пикового туза, вероятность этого события упадет до 1/36. Соответственно, если вы хотите вытащить из колоды любого туза, вероятность повысится в 4 раза и составит уже 4/36, т.е. 1/9.
Значительно сложнее вычислить вероятность выпадения определенных комбинаций карт. Этим подробно занимается теория вероятностей и комбинаторика.
Для проверки умозаключений, построенных по принципу обратной дедукции, в классической логике нет специальных правил. Это обусловлено тем, что классическая логика в своей основе дедуктивна и работает преимущественно с необходимо истинными и необходимо ложными конструкциями.
Тем не менее, перестраивая «обратнодедуктивные» умозаключения в дедуктивные, мы имеем возможность проверять их правдоподобность. Также, мы можем осуществлять проверку подобных умозаключений средствами модальной (алетической) логики.
Разберём означенное умозаключение
|
Все философы – грешны |
| Правдоподобно, что все философы – люди, а люди – грешные |
Для начала, вспомним практику построения таблиц истинности и попробуем (игнорируя кванторы) проверить это выражения средствами логики высказываний.
В логике высказываний данное выражение, вероятно, должно быть записано так: «(a⊃c)⊨(a⊃b)˄(b⊃c)».
Строим таблицу истинности:
| (a | ⊃ | c) | ⊃ | (a | ⊃ | b) | ˄ | (b | ⊃ | c) |
| И | И | И | И | И | И | И | И | И | И | И |
| И | Л | Л | И | И | И | И | Л | И | Л | Л |
| И | И | И | Л | И | Л | Л | Л | Л | И | И |
| И | Л | Л | И | И | Л | Л | Л | Л | И | Л |
| Л | И | И | И | Л | И | И | И | И | И | И |
| Л | И | Л | Л | Л | И | И | Л | И | Л | Л |
| Л | И | И | И | Л | И | Л | И | Л | И | И |
| Л | И | Л | И | Л | И | Л | И | Л | И | Л |
Из таблицы истинности мы видим, что умозаключение представляем выполнимую формулу. Значит, рассуждение правильное (или, по крайней мере, весьма правдоподобное). Тем не менее, мы опустили кванторы, и, следовательно, не учли всех необходимых деталей.
Если мы попробуем доказывать правдоподобность данного выражения путем построения натурального вывода, то нам придется доказывать формулу
∀x(F(x)⊃G(x))⊨◊(∀x(F(x)⊃L(x))˄∀x(L(x)⊃G(x)))
Понятно, что доказать такую формулу методом от противного не получится (причем, ни в классической системе натурального вывода, ни в модальной). А для того, чтобы доказать её в таком виде с помощью допущений, нам придётся предположить существование «L(x)», что сделает доказательство формулы ничтожным. Как же быть?
Вероятнее всего, учитывая, что мы имеем дело с выражениями, построенными методом обратной дедукции, нам всё равно придётся «перестраивать» их до полноценных дедуктивных выражений. Алгоритм таков:
- Мы меняем местами посылки и вывод;
- Доказываем получившееся дедуктивное выражение;
- На основании доказательства делаем вывод о правдоподобности исходного выражения, построенного методом обратной дедукции.
Соответственно, если, «перестраивая» выражение, мы получаем силлогизм, то можем проверить его по правилам силлогистики. Если получаем выражение, характерное для непосредственных выводов из простых суждений, то вспоминаем логический квадрат, законы превращения, обращения и противопоставления.
Предположим, дано умозаключение «Некоторые философы – невменяемы, поскольку все философы люди, а среди людей встречаются сумасшедшие».
На первый взгляд, вполне правдоподобно. Однако, давайте проверим.
| Некоторые философы невменяемы |
| Все философы – люди
Некоторые люди — невменяемы |
Перестраивая выражение в силлогизм, получаем:
| Все философы+ — люди— |
| Некоторые люди— невменяемы— |
| Некоторые философы— — невменяемы— |
Мы видим, что нарушено правило – средний термин не распределен ни в одной из посылок. Из этого делаем вывод: умозаключение «Некоторые философы – невменяемы, поскольку все философы люди, а среди людей встречаются сумасшедшие» — неправдоподобно.
Этот же силлогизм мы можем проверить в системе натурального вывода:
∀x(F(x)⊃L(x))˄∃x(L(x)˄N(x))⊃∃x(F(x)˄N(x))
Попробуем решить от противного:
- + ¬(∀x(F(x)⊃L(x))˄∃x(L(x)˄N(x))⊃∃x(F(x)˄N(x)))
- ∀x(F(x)⊃L(x))˄∃x(L(x)˄N(x))˄¬∃x(F(x)˄N(x)) – из 1 по О⊃
- ∃x(L(x)˄N(x)) – из 2 по У˄
- ∀x(F(x)⊃L(x)) — из 2 по У˄
- ¬∃x(F(x)˄N(x)) – из 2 по У˄
- L(x)˄N(x) – из 3 по У∃ — х ограничен
- ∀x¬(F(x)˄N(x)) – из 5 по О∃
- ¬(F(x)˄N(x)) – из 7 по У∀
- ¬F(x)˅¬N(x) – из 8 по О˅
- L(x) – из 6 по У˄
- N(x) – из 6 по У˄
- ¬F(x) – из 11 и 9 по У˅
- F(x)⊃L(x) – из 4 по У∀
- ?
Задача не решается. Силлогизм не является тождественно-истинной формулой. Попробуем решить задачу путем предположения некоторых допущений:
- 1. + ∀x(F(x)⊃L(x))
- + ∃x(L(x)˄N(x))
- F(x)⊃L(x) – из 1 по У∀
- L(x)˄N(x) – из 2 по У∃ — x ограничен
- L(x) – из 4 по У˄
- N(x) – из 4 по У˄
- ?
Решение задачи не ладится. Конечно, мы имеем право предположить, что «существует качество философии»:
- + F(x)
- F(x)˄N(x) — из 7 и 6 по В˄
- ∃x(F(x)˄N(x)) – из 8 по В∃
- ∀x(F(x)⊃L(x))˄∃x(L(x)˄N(x)) – из 1 и 2по В˄
- ∀x(F(x)⊃L(x))˄∃x(L(x)˄N(x))⊃∃x(F(x)˄N(x)) – из 10 и 9 по В⊃
Задача решена. Это означает, что при определенных обстоятельствах и допущениях, умозаключение «Некоторые философы – невменяемы, поскольку все философы люди, а среди людей встречаются сумасшедшие» — может быть правдоподобным.
Как же так? Согласно правилам силлогистики данное выражение ложно, а с точки зрения натурального исчисления, при определенных обстоятельствах, это же выражение становится правдоподобным?
На самом деле здесь нет противоречия.
Во-первых, неправильные силлогизмы, как мы уже говорили ранее, могут давать истинный результат, но не гарантируют его. Во-вторых, выполнимость формулы в натуральном исчислении также говорит нам о том, что формула не всегда, а при определенных обстоятельствах.
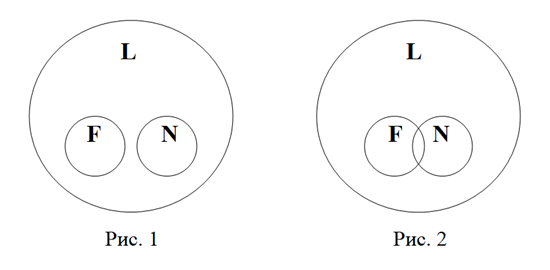
Лучше всего это можно проиллюстрировать на кругах Эйлера. Формула вида
∀x(F(x)⊃L(x))˄∃x(L(x)˄N(x))⊃∃x(F(x)˄N(x))
или, что одно и то же, вида
|
F+ — L— |
| L— — N— |
| F— — N— |
можно отразить на кругах Эйлера двояким способом:
На рисунках хорошо видно, что в одном случае круги F и N пересекаются, а в другом нет. При этом на обоих рисунках условие задачи отображено корректно.
Дополнительная информация
| Если вероятность события B при условии истинного A более ½ — мы говорим о наличии позитивной релевантности между A и B.
Если вероятность события B при условии истинного A менее ½ — мы говорим о наличии негативной релевантности между A и B. Если вероятность события B при условии истинного A равно ½ — мы говорим об отсутствии релевантности между A и B. |
- Обобщающая индукция
Обобщающей индукцией называется вывод о некотором классе на основании анализа его элементов.
Соответственно, обобщающую индукцию разделяют на полную и неполную, в зависимости от того, все элементы класса мы исследовали или нет.
Общая схема обобщающей индукции выглядит следующим образом:
| S1 суть P
S2 суть P S3 суть P S4 суть P ……………. Sn суть P |
| Все S суть P
|
Если мы удостоверились, что все Sn суть P, то вывод Все S суть P является необходимо истинным и он построен методом полной обобщающей индукции.
Если мы удостоверились, что лишь некоторые Sn суть P, то вывод Все S суть P является правдоподобным (вероятным) и он построен методом неполной обобщающей индукции.
На естественный язык это можно перевести так:
Если все без исключения студенты группы «Юриспруденция» знают логику, значит, вся группа Юриспруденции знает логику. Вывод сделан на основе полной обобщающей индукции, и он истинен.
Если некоторые студенты группы «Юриспруденция» знают логику, значит, вероятно, вся группа Юриспруденции знает логику. Вывод сделан на основе неполной обобщающей индукции, и он правдоподобен.
Неполная индукция – один из самых распространенных эмпирических методов в науке, поскольку проверить все без исключения события, как правило, невозможно. Этот метод является основным при проведении социологических исследований.
Представим, что мы хотим доказать факт того, что камень, подкинутый в воздух, обязательно полетит вниз. Если мы будем обосновывать это событие, исходя из закона всемирного тяготения, то докажем его с абсолютной истинностью. Потому что в этом случае мы используем дедукцию и выводим из общего закона его частный случай.
Но представим, что закон всемирного тяготения нам неизвестен. Тогда нам остается доказывать, что камень, подкинутый в воздух, обязательно полетит вниз, экспериментально. Мы будем тысячи, миллионы, миллиарды раз подкидывать этот несчастный камень, но в итоге сможем сделать лишь правдоподобный вывод – весьма вероятно, камень, подкинутый в воздух, полетит вниз. Потому что в случае экспериментального доказательства мы используем неполную обобщающую индукцию.
Дополнительная информация
| По большому счету, можно оспорить любой вывод как необходимо истинный на том основании, что все существующие законы – результат эмпирических наблюдений. Таким образом, любой закон представляет собой вывод, построенный путём неполной индукции. А, раз любой закон имеет лишь вероятностный характер, следовательно, и дедуктивные выводы из него не могут быть необходимо истинными. |
- Выводы по аналогии
Вывод по аналогии строится путем сравнения свойств двух или нескольких объектов. Если большинство свойств сравниваемых объектов совпадает, мы делаем вывод, что и остальные свойства у них одинаковы.
Общая схема выводов по аналогии выглядит так:
| A обладает признаками P1 P2 P3 P4 и S
B обладает признаками P1 P2 P3 P4 |
| Вероятно, B обладает также признаком S
|
