X. Натуральные исчисления в модальной логике

Урок X.

Натуральные исчисления в модальной логике.

Для натуральных исчислений в модальной логике используются все законы и правила исчисления логики высказываний. К ним прибавляются правила кванторов и специальные правила модальной логики. В этом смысле, натуральное исчисление в модальной логике является расширением натурального исчисления логики предикатов.

Итак, напомним правила логики высказываний:

Правила вывода первого рода:

1. а,b ⊧ a˄b –введение ˄ — конъюнкции — (кратко: В˄)

Поясняем. Знак «⊧» означает логическое следование и читается «следовательно». Название правила «введение конъюнкции» кратко обозначается, как «В˄». Далее, по аналогии:

2. a˄b ⊧ а – удаление (исключение) конъюнкции ˄ (кратко У˄)
3. ¬(a˄b) ⊧ ¬a∨¬b — отрицание ˄ (кратко О˄)
4. а⊧ а˅b – введение ˅ (В˅)
5. а˅b, ¬a ⊧ b — удаление ˅ (У˅)
6. ¬(а˅b) ⊧¬a∧¬b — отрицание ˅ (О˅)
7. а⊃b, a) ⊧ b – удаление ⊃ (У⊃)¹
8. а⊃b, ¬b) ⊧ ¬a– удаление ⊃ (У⊃)²
9. a, b ⊧ (а⊃b), (b⊃a) — введение ⊃ (В⊃)
10. ¬(а⊃b) ⊧ a˄¬b — отрицание ⊃ (О⊃)
11. а⊃b, b⊃a ⊧ a≡b — введение ≡ (В≡)
12. a≡b ⊧ а⊃b, b⊃a — удаление ≡ (У≡)
13. а⊧ ¬¬а — введение двойного отрицания (В¬¬)
14. ¬¬а⊧ а — удаление двойного отрицания (У¬¬)

Правила вывода второго рода (которые нужны в любом случае):

((а⊃с)˄(b⊃с)) ⊧ (а˅b) →с – рассуждение разбором случаев (РРС)

(b˄¬b⊃а) ⊧ ¬а – сведение к абсурду (СА)

(¬а⊃ (b˄¬b)) ⊧ а – доказательство от противного (ДОП)

(Г, a⊧ b) ⊧ (Г⊧ a→b) — правило дедукции. Читается: если из множества гипотез Г и посылки а логически следует b, то из множества гипотез Г логически следует a⊃b.

Что касается правил кванторов  (с помощью которых мы осуществляли исчисления предикатов), то мы можем выбрать систему натурального вывода:

1. ∀xP(x)⊃P(t) – схема удаления ∀(У∀)
2. P(t)⊃ ƎхP(x) – схема введения Ǝ (ВƎ)
3. P(t)⊃∀xP(x) — схема введения ∀ (В∀)
4. ƎxP(x)⊃P(t) – схема удаления Ǝ (УƎ)

Или же, можем использовать аксиоматическую систему:

∀xP(x) ⊃P(t) – схема удаления ∀ (У∀)

P(t)⊃ƎхP(x) – схема введения Ǝ (ВƎ)

∀x(А⊃P(x))⊃(А⊃∀P(х)) – схема введения ∀ в консеквент.

∀x(P(x)⊃А)⊃(ƎхP(х)⊃А) – схема введения Ǝ в антецедент.

P(t)⊃∀xP(x) — правило обобщения.

Добавляем специальные правила натурального вывода модальной логики:

□A→A – правило удаления необходимости (У□)

A→ ◊A –- введение возможности (В◊)

¬□A→¬◊A – отрицание необходимости (О□)

¬◊A→□¬A – отрицание возможности (О◊)

□(A˄B)→□A˄□B – введение необходимости в конъюнкции (В□˄)

□A˄□B→□(A˄B) – удаление необходимости из конъюнкции (У□˄)

◊(A˅B)→ ◊A˅◊B – введение возможности в дизъюнкцию (В◊˅)

◊A˅◊B→◊(A˅B) – удаление возможности из дизъюнкции (У◊˅)

□A˅□B→□(A˅B) – удаление необходимости из дизъюнкции (У□˅)

◊(A˄B)→◊A˄◊B – введение возможности в конъюнкцию (В◊˄)

□(A⊃B)→□A⊃□B – введение необходимости в импликацию (В□⊃)

□A→□□A – введение дополнительной необходимости (В□□)

□∀xA(x)→∀x□A(x) – перестановка необходимости от всеобщности (∀□)

∀x□A(x)→□∀xA(x) – перестановка необходимости к всеобщности (□∀)

◊∃xA(x)→ ∃x◊A(x) — перестановка возможности от существования (∃◊)

∃x◊A(x)→◊ ∃xA(x) – перестановка возможности к существованию (◊∃)

◊A→□◊A – введение необходимости возможности (В□◊)

◊A, □B→◊(A˄B) — замена необходимости на возможность (З□◊)

(A↔B)→□(A↔B) – введение необходимой эквивалентности (В□↔)

□(A↔B)→(A↔B) – удаление необходимой эквивалентности (У□↔)

Правило второго рода:

A→□A – правило введения необходимости (В□) – правило Гёделя

Имеет смысл вспомнить эквивалентности:

□A⇔¬◊¬A

◊A⇔¬□¬A

∇A⇔◊A˄◊¬A

а также отрицания:

¬□А⇔◊¬ A;

¬◊A⇔□¬А;

¬∇А⇔□А∨□¬A

Предположим, дана выводимость

□∀x(A(x)⊃В(x))⊃□∀x(□A(x)⊃◊B(x)).

Попробуем доказать эту формулу от противного и предположим:

+¬(□∀x(A(x)⊃В(x))⊃□∀x(□A(x)⊃◊B(x)))

□∀x(A(x)⊃В(x)) – из 1 по О⊃

∀x□(A(x)⊃В(x)) – из 2 по ∀□

□(A(x)⊃В(x)) – из 3 по У∀

A(x)⊃В(x) – из 4 по У□

¬(□∀x(□A(x)⊃◊B(x))) — из 1 по О⊃

□∀x□A(x) – из 6 по О⊃

¬□∀x◊B(x) — из 6 по О⊃

¬◊∀x◊B(x) – из 8 по О□

□¬∀x◊B(x) – из 9 по О◊

¬∀x◊B(x) – из 10 по У□

∃х¬◊B(x) – из 11 по О∀

¬◊B(x) – из 12 по У∃ — х ограничена

□¬B(x) – из 13 по О◊

¬B(x) – из 14 по У□

∀x□A(x) – из 7 по У□

□A(x) – из 16 по У∀

A(x) – из 17 по У□

В(x) – из 5 и 18 по У⊃

В(x)˄¬B(x) – из 19 и 15 по В˄

(В(x)˄¬B(x))⊃¬(□∀x(A(x)⊃В(x))⊃□∀x(□A(x)⊃◊B(x))) —  из 20 и 1 по В⊃ (или по правилу дедукции)

□∀x(A(x)⊃В(x))⊃□∀x(□A(x)⊃◊B(x)) – из 21 по ДОП. ■

Решение задачи путём построения семантической таблицы:

В качестве еще одного примера, попробуем разобрать выводимость ⊧ □∀x□(P(x)˄S(x))˅◊∃x(◊¬P(x)˄◊S(x))˅¬◊∀x(P(x)˄¬S(x))˅

˅□∃x(□¬P(x)˄◊¬S(x)).

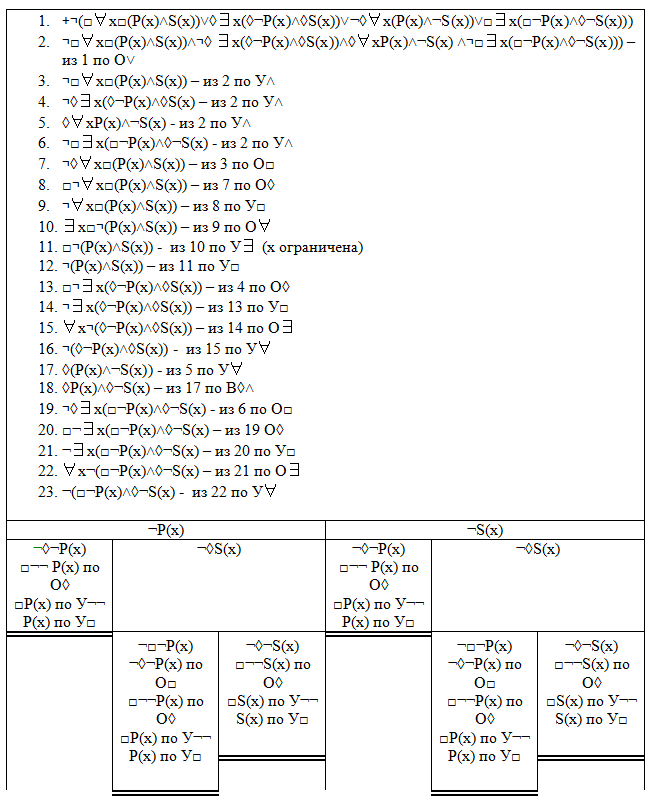
Начиная с 23 действия, мы могли бы эстетически построить таблицу по-другому:

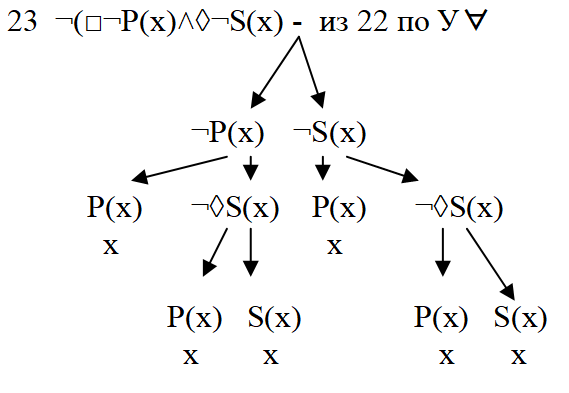
Или, что то же самое, в классической системе натурального вывода:

1. +¬(□∀x□(P(x)˄S(x))˅◊∃x(◊¬P(x)˄◊S(x))˅¬◊∀x(P(x)˄¬S(x))˅
   ˅□∃x(□¬P(x)˄◊¬S(x)))
2. ¬□∀x□(P(x)˄S(x))˄¬◊ ∃x(◊¬P(x)˄◊S(x))˄◊∀xP(x)˄¬S(x)˄

˄¬□∃x(□¬P(x)˄◊¬S(x))) – из 1 по О˅

3. ¬□∀x□(P(x)˄S(x)) – из 2 по У˄
4. ¬◊∃x(◊¬P(x)˄◊S(x) – из 2 по У˄
5. ◊∀xP(x)˄¬S(x) — из 2 по У˄
6. ¬□∃x(□¬P(x)˄◊¬S(x) — из 2 по У˄
7. ¬◊∀x□(P(x)˄S(x)) – из 3 по О□
8. □¬∀x□(P(x)˄S(x)) – из 7 по О◊
9. ¬∀x□(P(x)˄S(x)) – из 8 по У□
10. ∃x□¬(P(x)˄S(x)) – из 9 по О∀
11. □¬(P(x)˄S(x)) —  из 10 по У∃ (x ограничена)
12. ¬(P(x)˄S(x)) – из 11 по У□
13. □¬∃x(◊¬P(x)˄◊S(x)) – из 4 по О◊
14. ¬∃x(◊¬P(x)˄◊S(x)) – из 13 по У□
15. ∀x¬(◊¬P(x)˄◊S(x)) – из 14 по О∃
16. ¬(◊¬P(x)˄◊S(x)) —  из 15 по У∀
17. ◊(P(x)˄¬S(x)) — из 5 по У∀
18. ◊P(x)˄◊¬S(x) – из 17 по В◊˄
19. ¬◊∃x(□¬P(x)˄◊¬S(x) — из 6 по О□
20. □¬∃x(□¬P(x)˄◊¬S(x) – из 19 О◊
21. ¬∃x(□¬P(x)˄◊¬S(x) – из 20 по У□
22. ∀x¬(□¬P(x)˄◊¬S(x) – из 21 по О∃
23. ¬(□¬P(x)˄◊¬S(x) —  из 22 по У∀
24. ◊P(x) – из 18 по У˄
25. ◊¬S(x) – из 18 по У˄
26. ¬P(x) ˅¬S(x)) – из 12 по О˄
27. ¬◊¬P(x)˅¬◊S(x)) —  из 16 по О˄
28. ¬□¬P(x)˅¬◊¬S(x) —  из 23 по О˄
29. ¬□¬P(x) из 25 и 28 по У˅
30. ¬◊¬P(x) из 29 по О□
31. □¬¬P(x) из 30 по О◊
32. P(x) из 31 по У¬¬ и У□
33. S(x)) из 26 и 32 по У˅
34. ¬P(x) – из 33 и 26 по У˅
35. P(x)˄¬P(x) из 32 и 34 по В˄
36. (P(x)˄¬P(x))⊃¬(□∀x□(P(x)˄S(x))˅◊∃x(◊¬P(x)˄◊S(x))˅ ˅¬◊∀x(P(x)˄¬S(x))˅□∃x(□¬P(x)˄◊¬S(x))) из 35 и 1 по В⊃
37. □∀x□(P(x)˄S(x))˅◊∃x(◊¬P(x)˄◊S(x))˅¬◊∀x(P(x)˄¬S(x))˅

˅□∃x(□¬P(x)˄◊¬S(x)) – из 36 по ДОП.

Мы специально прописали вывод максимально подробно, чтобы читатель обратил внимание, что многие последовательности выводов часто повторяются. Например,

• ¬□¬P(x) из 25 и 28 по У˅
• ¬◊¬P(x) из 29 по О□
• □¬¬P(x) из 30 по О◊
• P(x) из 31 по У¬¬ и У□

или

• ¬□∀x□(P(x)˄S(x))
• ¬◊∀x□(P(x)˄S(x))
• □¬∀x□(P(x)˄S(x))
• ¬∀x□(P(x)˄S(x))

Такие последовательности позволяют нам самим создавать выводы второго рода.

В первом случае, это ¬□¬A→A и  ¬◊¬A→A; во втором — ¬□A→¬A и ¬◊A→¬A

Из практики исчислений можно добавить правила второго рода (схемы аксиом):

A→□A – правило введения необходимости (В□) – правило Гёделя
¬□A→□¬A
¬□A→¬A
¬□А→◊¬A
¬□¬A→◊A
□A→¬◊¬A
□¬А→¬◊A
¬◊A→¬A
¬◊¬A→□A
¬◊¬A→A
◊A→¬□¬A
◊¬A→¬□А

Попробуем решетить еще одну задачу. Правильным ли является рассуждение «Некоторые  испанцы в обед обязательно едят гаспачо. Любое гаспачо всегда готовится из томатов. Из этого следует, что некоторые испанцы, скорее всего, неравнодушны к помидорам»?

Попробуем перевести это умозаключение на формальный язык логики.

Некоторые испанцы в обед обязательно едят гаспачо.

Слово «некоторые» говорит нам, что необходим квантор существования. А слово «обязательно» намекает на знак необходимости:

▢∃x(I(x)˄G(x))

В принципе, сразу используя правило удаления необходимости, мы можем записать:

∃x(I(x)˄G(x))

Любое гаспачо всегда готовится из томатов:

▢∀x(G(x)⊃T(x))

Соответственно, снова используя правило удаления необходимости, получаем

∀x(G(x)⊃T(x))

Некоторые испанцы, скорее всего, неравнодушны к помидорам:

◊∃x(I(x)˄T(x))

В итоге получаем выводимость

⊨∃x(I(x)˄G(x))˄∀x(G(x)⊃T(x))⊃◊∃x(I(x)˄T(x))

Итак, дано:

⊨∃x(I(x)˄G(x))˄∀x(G(x)⊃T(x))⊃◊∃x(I(x)˄T(x))

1. + ∃x(I(x)˄G(x))
2. + ∀x(G(x)⊃T(x))

В качестве гипотез мы использовали посылки для построения заданного вывода «◊∃x(I(x)˄T(x))».

3. I(x)˄G(x) – из 1 по У∃ — х ограничен
4. G(x)⊃T(x) – из 2 по У∀
5. I(x) – из 3 по У˄
6. G(x) – из 3 по У˄
7. T(x) – из 4 и 6 по У⊃
8. I(x)˄T(x) – из 5 и 7 по В˄
9. ∃x(I(x)˄T(x)) – из 8 по В∃
10. ◊∃x(I(x)˄T(x)) — из 9 по В◊

Теперь мы получили искомый вывод. На этом исчисление можно закончить. Однако, для формального завершения можно дописать еще пару действий:

11. ∃x(I(x)˄G(x))˄∀x(G(x)⊃T(x)) – из 1 и 2 по В˄
12. ∃x(I(x)˄G(x))˄∀x(G(x)⊃T(x))⊃◊∃x(I(x)˄T(x)) из 10 и 11 по В⊃ (или правилу дедукции). ∎

Важно

Конечно, логика стремится к определенности, предпочитаю необходимые события вероятным. В точной науке вероятных событий принято избегать. Скажем, утверждение химика о том, что некая реакция может произойти, а может и не произойти – мало информативна.

Другое дело – гуманитарные науки и реальные жизненные обстоятельства. Здесь сама возможность некого события может иметь большое значение. Например, вывод о том, что в ближайшей перспективе возможно социальное потрясение, может в корне изменить внутреннюю политику государства. Для полицейского, задерживающего преступника, информация, что преступник возможно вооружен, может спасти ему жизнь.