Урок VII.
Семантические таблицы.
Существует еще один эффективный способ проверки формул на истинность и ложность – построение семантических таблиц или таблиц Бэта (в честь Эверта Бэта – создателя данного метода).
Считается, семантические таблицы не работают там, где необходимо проанализировать формулы, содержащие знаки эквивалентности и строгой дизъюнкции. Это действительно так. Но кто нам мешает путём эквивалентных преобразований «перестроить» формулу и избавиться от знаков эквивалентности и строгой дизъюнкции?
Для этого весь полезными будут следующие эквивалентные преобразования:
приведение формул к импликации —
(a˄b)≡¬(a⊃¬b)∧¬(b⊃¬a)
(a˅b)≡(¬a⊃b)∧(¬b⊃a)
(a≡b)≡(a⊃b)∧(b⊃a)
(a˅b)≡(¬a⊃b)∧(¬b⊃a)
приведение формул к конъюнкции —
(a⊃b)≡¬(a˄¬b)
(a˅b)≡¬(¬a˄¬b)
(a˅b)≡¬((a∨¬b)∧(¬a∨b))
(a≡b)≡(a∨¬b)˄(b∨¬a)
приведение формул к дизъюнкции —
(a˄b)≡¬(¬a∨¬b)
(a⊃b)≡(¬a∨b)
(a˅b)≡(a˄¬b)∨(¬a˄b)
(a≡b)≡(a∧b)∨(¬a˄¬b)
Для начала повторим правила (описанные в различных учебниках), затем поясним методику построения тоблиц.
Для построения семантических таблиц созданы специальные правила редукции.
¬Л. Если формула ¬A имеется в левом столбце таблицы (подтаблицы), то в правом столбце той же таблицы (подтаблицы) пишем А
¬Пр. Если формула ¬A имеется в правом столбце, то в левом столбце пишем А
∧Л. Если формула А∧В имеется в левом столбце таблицы (подтаблицы), то в том же столбце пишем формулы А и В.
∧Пр. Если формула А∧В находится в правом столбце таблицы (подтаблицы), то в каждом из столбцов образуем две новые альтернативные подтаблицы этого столбца и в левой подтаблице правого столбца пишем А, а в правой таблице того же столбца – В.
∨Л. Если формула A∨B находится в левом столбце таблицы (подтаблицы), то в каждом из столбцов образуем две новые альтернативные подтаблицы и в левой из них (левого столбца) пишем А, а в правой (того же столбца) – В.
∨Πр. Если формула А∨В находится в правом столбце таблицы (подтаблицы), то в том же столбце пишем формулы А и В.
⊃Л. Если формула А⊃В находится в левом столбце таблицы (подтаблицы), то в каждом из столбцов образуем две новые альтернативные подтаблицы и в правой подтаблице левого столбца пишем формулу В, а в левой подтаблице правого столбца пишем А.
⊃Пр. Если формула Α⊃Β находится в правом столбце таблицы (подтаблицы), то в левом столбце той же таблицы пишем формулу A, а в правом – В.
∀Л. Если формула ∀αA(α) находится в левом столбце таблицы (подтаблицы), то в том же столбце помещаем формулу Α(β), где β – произвольная индивидная переменная или константа, Α(β) есть результат правильной подстановки β вместо α в А(α). Эвристический совет: в качестве β нужно взять индивидную константу, которая уже встречается в подтаблице, или переменную, которая имеет свободные вхождения в какую-то из формул подтаблицы; если таковых нет, то вводится произвольная индивидная константа.
∀Пр. Если формула ∀αA(α) находится в правом столбце таблицы (подтаблицы), то в тот же столбец помещаем формулу А(β), где β – новая индивидная константа, т.е. константа, не встречающаяся еще ни в левом, ни в правом столбцах, а А(β) есть результат правильной подстановки β в А(α) вместо α.
ƎЛ. Если формула ƎαА(α) находится в левом столбце таблицы (подтаблицы), то в тот же столбец помещаем формулу А(β), где β – новая индивидная константа; А(β) – результат правильной подстановки индивидной константы β в А(α) вместо α.
ƎПр. Если формула Ǝα A(α) находится в правом столбце таблицы (подтаблицы), то в тот же столбец помещаем формулу А(β), где β – произвольная индивидная переменная или константа, а А(β) – то же, что и в пояснении к правилу ∀Л. Эвристический совет тот же, что описан при формулировке правила ∀Л.
Альтернативная подтаблица (а если таковых нет, то таблица) является замкнутой, если некоторая формула входит в ее левый и правый столбцы. Таблица является замкнутой, если замкнуты все ее альтернативные подтаблицы.
Предположим, дано:
∀х(Р(х)⊃Q(x))∧∀x(R(x,a)⊃¬Q(x))∧∀x(¬P(x)⊃¬S(x))╞∀х(R(х,a)⊃¬S(x)).
Первой, второй и третьей посылками являются формулы: ∀х(Р(х)⊃Q(x)), ∀x(R(x,a)⊃¬Q(x)), ∀x(¬P(x)⊃¬S(x)), а заключением – формула ∀х(R(х,a)⊃¬S(x)). Строя семантическую таблицу, в левый столбец пишем формулы, соответствующие посылкам, а в правый – формулу, соответствующую заключению. Далее применяем правила редукции:
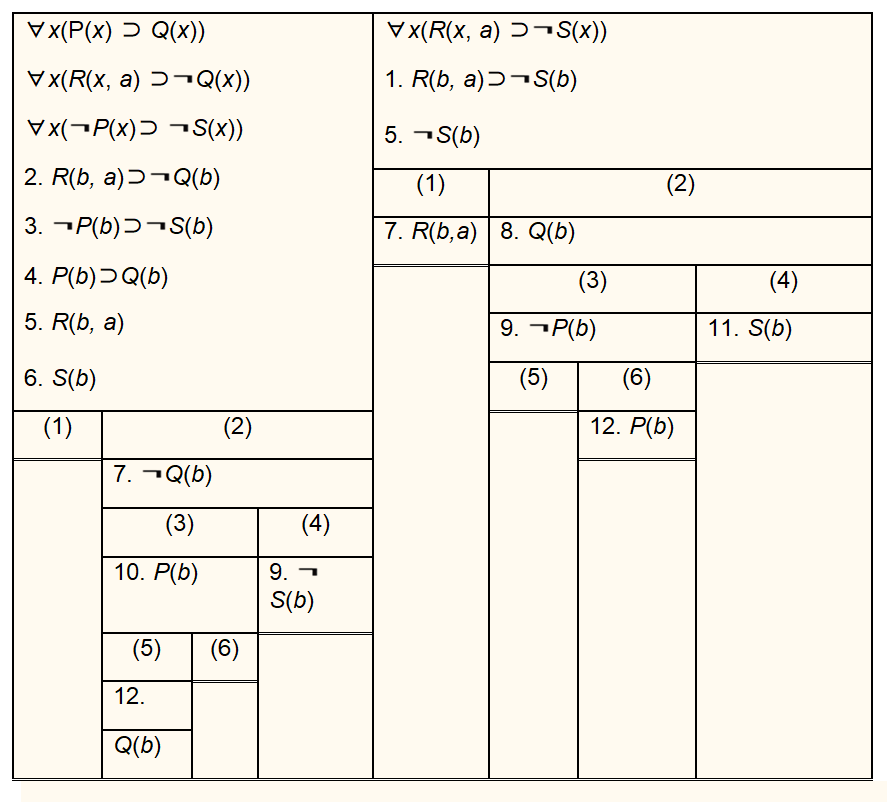
Важно
| С нашей точки зрения, семантические таблицы проще строить в сокращенном виде, не используя такое количество правил редукции (только эквивалентности) и, особо не увлекаясь дроблением ветвей таблицы. |
Ту же самую задачу можно было отразить проще:

Совет
| Главное, надо понять логику построения семантических таблиц:
— если мы имеем конъюнкцию — a˄b, то вписываем в выводе «a» и «b», не размножая таблицу; — если мы имеем дизъюнкцию — a˅b, то размножаем таблицу и в одном столбце пишем «а», а в другом – «b». Все остальные формулы мы преобразуем в конъюнкцию или дизъюнкцию по эквивалентностям: (a⊃b)→ ¬a˅b ¬(a⊃b)→ a˄¬b ¬(a˄¬b)→ ¬a˅¬b ¬(a˅¬b)→ ¬a˄¬b |
Попробуем подробно решить ещё одну задачу. Необходимо обосновать выводимость
Ǝх(Р(х)˄R(x)), ∀x(R(x)⊃S(x))╞ Ǝх(S(х)˄P(x)).
Всегда рассуждаем методом от противного.
Предположим, что выводимость не верна:
Ǝх(Р(х)˄R(x))˄∀x(R(x)⊃S(x))╞ ¬Ǝх(S(х)˄P(x)).
| 1. Ǝх(Р(х)˄R(x))
2. ∀x(R(x)⊃S(x)) 3. ¬Ǝх(S(х)˄P(x)) |
Следующим шагом пытаемся «избавиться» от кванторов:
| 1. Ǝх(Р(х)˄R(x))
2. ∀x(R(x)⊃S(x)) 3. ¬Ǝх(S(х)˄P(x)) 4. Р(х)˄R(x) – из 1 по УƎ – x ограничена 5. R(x)⊃S(x) — из 2 по У∀ 6. ∀x¬(S(x)˄P(x)) – из 3 по ОƎ 7. ¬(S(x)˄P(x)) – из 6 по У∀ |
Теперь смотрим, какие формулы мы можем еще получить, не размножая таблицу. Очевидно, из действия 4 мы можем получить две формулы путем удаления конъюнкции:
| 1. Ǝх(Р(х)˄R(x))
2. ∀x(R(x)⊃S(x)) 3. ¬Ǝх(S(х)˄P(x)) 4. Р(х)˄R(x) – из 1 по УƎ – x ограничена 5. R(x)⊃S(x) — из 2 по У∀ 6. ∀x¬(S(x)˄P(x)) – из 3 по ОƎ 7. ¬(S(x)˄P(x)) – из 6 по У∀ 8. P(x) – из 4 по У˄ 9. R(x) — из 4 по У˄ |
Далее придется размножать таблицу, поскольку формулы R(x)⊃S(x) (№5) и ¬(S(x)˄P(x)) (№7) путем эквивалентных преобразования превращаются в дизъюнкции – «¬R(x)˅S(x)» и «¬S(x)˅¬P(x)». С какой именно из них начинать – значения не имеет. Давайте начнём с «¬R(x)˅S(x)»:
| 1. Ǝх(Р(х)˄R(x))
2. ∀x(R(x)⊃S(x)) 3. ¬Ǝх(S(х)˄P(x)) 4. Р(х)˄R(x) – из 1 по УƎ – x ограничена 5. R(x)⊃S(x) — из 2 по У∀ 6. ∀x¬(S(x)˄P(x)) – из 3 по ОƎ 7. ¬(S(x)˄P(x)) – из 6 по У∀ 8. P(x) – из 4 по У˄ 9. R(x) — из 4 по У˄ |
|
|
¬R(x)
|
S(x) |
Получаем первое противоречие: R(x) в действии №9 и ¬R(x) в подтаблице. Чтобы зафиксировать это противоречие, замкнем подтаблицу:
| 1. Ǝх(Р(х)˄R(x))
2. ∀x(R(x)⊃S(x)) 3. ¬Ǝх(S(х)˄P(x)) 4. Р(х)˄R(x) – из 1 по УƎ – x ограничена 5. R(x)⊃S(x) — из 2 по У∀ 6. ∀x¬(S(x)˄P(x)) – из 3 по ОƎ 7. ¬(S(x)˄P(x)) – из 6 по У∀ 8. P(x) – из 4 по У˄ 9. R(x) — из 4 по У˄ |
||
|
¬R(x) __________ |
S(x)
|
|
В оставшуюся ветку таблицы вписываем последние формулы
| 1. Ǝх(Р(х)˄R(x))
2. ∀x(R(x)⊃S(x)) 3. ¬Ǝх(S(х)˄P(x)) 4. Р(х)˄R(x) – из 1 по УƎ – x ограничена 5. R(x)⊃S(x) — из 2 по У∀ 6. ∀x¬(S(x)˄P(x)) – из 3 по ОƎ 7. ¬(S(x)˄P(x)) – из 6 по У∀ 8. P(x) – из 4 по У˄ 9. R(x) — из 4 по У˄ |
||
|
¬R(x) ________ |
S(x)
|
|
| ¬S(x) |
¬P(x) |
|
Видим противоречие «¬S(x)» и «S(x)» — замыкаем подтаблицу.
Видим противоречие «¬P(x)» и «P(x)» (из действия №8) – замыкаем таблицу.
Все подтаблицы замкнуты:
| 1. Ǝх(Р(х)˄R(x))
2. ∀x(R(x)⊃S(x)) 3. ¬Ǝх(S(х)˄P(x)) 4. Р(х)˄R(x) – из 1 по УƎ – x ограничена 5. R(x)⊃S(x) — из 2 по У∀ 6. ∀x¬(S(x)˄P(x)) – из 3 по ОƎ 7. ¬(S(x)˄P(x)) – из 6 по У∀ 8. P(x) – из 4 по У˄ 9. R(x) — из 4 по У˄ |
||
|
¬R(x) _________ |
S(x)
|
|
| ¬S(x)
______ |
¬P(x) _____ |
|
В литературе можно встретить иной (с эстетической точки зрения) вид семантических таблиц. Последняя таблица может быть составлена так:
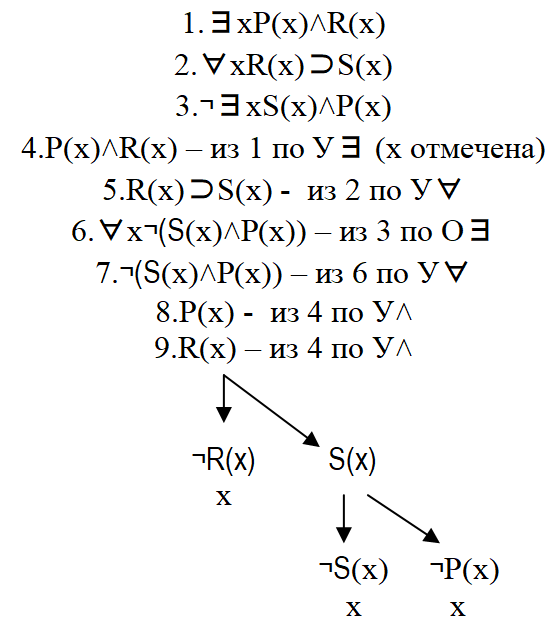
В этой форме написания семантической таблицы размножение таблицы обозначено стрелками, а замыкание знаком «х».
Поскольку таблица замкнулась, наше предположение о том, что формула не верна – ошибочно. Следовательно, выводимость
Ǝх(Р(х)˄R(x)), ∀x(R(x)⊃S(x)) ⊧ Ǝх(S(х)˄P(x)) – истинна.
Мы могли бы использовать формулы в другом порядке, но результат бы от этого не изменился:
| 1. Ǝх(Р(х)˄R(x))
2. ∀x(R(x)⊃S(x)) 3. ¬Ǝх(S(х)˄P(x)) 4. Р(х)˄R(x) – из 1 по УƎ – x ограничена 5. R(x)⊃S(x) — из 2 по У∀ 6. ∀x¬(S(x)˄P(x)) – из 3 по ОƎ 7. ¬(S(x)˄P(x)) – из 6 по У∀ 8. P(x) – из 4 по У˄ 9. R(x) — из 4 по У˄ |
||
|
¬S(x)
|
¬P(x)
_______ |
|
| ¬R(x)
________ |
S(x)
__________ |
|
Попробуем методом семантических таблиц проверить силлогизм. (Понятно, что семантические таблицы могут проверять не только силлогизмы – их функционал значительно шире):
| Логики используют семантические таблицы |
| Некоторые логики – поэты |
| Некоторые поэты используют семантические таблицы |
Данный силлогизм переводим на формальный язык: ∀x(S(x)⊃(P(х)), Ǝх(S(х)˄R(х))╞ Ǝх(R(х)˄P(х))
| 1. ∀x(S(x)⊃(P(х))
2. Ǝх(S(х)˄R(х)) 3. ¬Ǝх(R(х)˄P(х)) 4. S(x)⊃(P(х) – из 1 по У∀ 5. S(х)˄R(х)- из 2 по УƎ – х — ограничена 6. ∀x¬(R(х)˄P(х)) – из 3 по ОƎ 7. ¬(R(х)˄P(х)) – из 6 по У∀ 8. S(х) – из 5 по У˄ 9. R(х) – из 5 по У˄ |
||
|
¬S(x) ______ |
P(x) | |
| ¬R(х)
_______ |
¬P(x) _______ |
|
Нередко в зарубежной литературе можно встретить следующее написание:

Ради эксперимента, попробуем построить семантическую таблицу для неправильного силлогизма:
| Логики используют семантические таблицы |
| Некоторые логики – поэты |
| Все поэты используют семантические таблицы |
Выводимость, видимо, должна быть такой:
∀x(S(x)⊃ (P(х)), Ǝх(S(х) ˄R(х)) ⊧ ∀хR(х)⊃P(х))
| 1. ∀x(S(x)⊃(P(х))
2. Ǝх(S(х)˄R(х)) 3. ¬∀х(R(х)˄P(х)) 4. S(x)⊃(P(х) – из 1 по У∀ 5. S(х)˄R(х)- из 2 по УƎ – х ограничена 6. Ǝx¬(R(х)˄P(х)) – из 3 по ОƎ 7. ¬(R(х)˄P(х)) – из 6 по УƎ – х ограничена
|
«Х» ограничена дважды, следовательно доказать формулу не представляется возможным.
