Урок IV.
Синтаксис простых суждений.
Логика высказываний является важной, но достаточно узкой частью формальной логики. Как только мы переходим к логике предикатов (к анализу внутренней структуры суждений), логический анализ усложняется и начинается действительно творческая работа. Если в логике высказываний разрешимость логической системы очевидна (таблицы истинности являются алгоритмом проверки формул на истинность и ложность), то в логике предикатов подобного метода разрешимости логической системы не существует. И именно это делает логику предикатов особенно привлекательной.
Но, прежде чем перейти к исчислениям логики предикатов, необходимо разобраться в её синтаксисе.
Начнём с того, что в простом суждении есть субъект суждения (логическое подлежащее) и предикат (логическое сказуемое). Субъектом в логике называется объект, о котором мы что-то утверждаем или отрицаем. Например,
Иванов двоечник
Идёт дождь
Человек – не насекомое
Они – братья
Я – гений
«Иванов», «дождь», человек», «они», «Я» — субъекты данных высказываний. А то, что мы утверждаем или отрицаем о них – есть предикаты. Предикатами в нашем случае являются свойства и отношения «двоечник», «идёт», «не насекомое», «братья», «гений».
Любое простое высказывание имеет одинаковую структуру:
S – P
где «S» — субъект (логическое подлежащее), «P» — предикат (логическое сказуемое) и связка «-», читаемая как «есть», «суть», «является».
Перефразируя наши примеры, мы получаем высказывания логического типа:
Иванов суть двоечник
Дождь есть идущий
Человек не является насекомым
Они являются братьями
Я есмь гений
Важно
| В логике предикатов принято два способа написания простых высказываний: «Все S – P» и ∀x(S(x)⊃P(x)). Первое читается как «S суть P», второе как Для всех «х» верно, что, если он обладает свойством «S», то «x» обладает и свойством «P». Оба написания идентичны. Нам понадобятся оба написания, поскольку в различных разделах логики иногда удобно первое написание, а иногда – второе. |
Из приведённых примеров очевидно, что мы можем либо что-то утверждать об объекте, либо что-то о них отрицать. Поэтому суждения бывают как утвердительными, так и отрицательными (качественная характеристика суждения):
Все S суть P ∀x(S(x)⊃P(x))
Все S не суть P ∀x(S(x)⊃¬P(x))
Кроме того, мы можем что-то утверждать или отрицать как обо всех объектах, так и о некоторых. В этом смысле, суждения могут быть как общими, так и частными (количественная характеристика суждения):
Все S суть P ∀x(S(x)⊃P(x))
Некоторые S не суть P ∃x(S(x)∧¬P(x))
Таким образом, мы получаем всего четыре возможных варианта суждений:
| A | Обще-утвердительное | Все S суть P | ∀x(S(x)⊃P(x)) |
| E | Обще-отрицательное | Все S не суть P | ∀x(S(x)⊃¬P(x)) |
| I | Частно-утвердительное | Некоторые S суть P | ∃x(S(x)∧P(x)) |
| O | Частно-отрицательное | Некоторые S не суть P | ∃x(S(x)∧¬P(x)) |
Важно
| Для общих суждений (с квантором ∀) свойства объекта выражаются через импликацию «⊃», например, ∀x(S(x)⊃P(x)).
Для частных суждений (с квантором ∃) свойства объекта выражаются через конъюнкцию «∧», например, ∃x(S(x)∧P(x)). Выражение «Все люди млекопитающие» можно прочесть так: «Для всех людей верно, что, если они люди, то они млекопитающие». А выражение «Некоторые люди млекопитающие» можно прочесть так: «Для некоторых людей верно, что они люди и млекопитающие». Эту разницу необходимо запомнить. Строго говоря, кроме частных и общих суждений существуют еще единичные, объём которых исчерпывается одним объектом. Это такие суждения, как «Иванов – студент», «Москва – столица России», «Я шагаю по Москве» и т.д. Единичные суждения по своим свойствам идентичны общим суждениям. Также читатель должен иметь в виду, что любое общее суждение с истинностью преобразуется в частное (но не наоборот). Из выражения «Все люди млекопитающие» мы с истинностью выводим суждение «Некоторые люди млекопитающие» (точнее, «Существует хотя бы один человек-млекопитающее»). И, наконец, целесообразно запомнить, что, если в каком-либо высказывании отсутствует квантор, то по умолчанию принимается квантор общности. Из суждения «Люди – млекопитающие» мы с истинностью выводи суждение «Все люди млекопитающие». |
Между этими суждениями есть тесная взаимосвязь. Чаще всего эту взаимосвязь показывают на так называемом «логическом квадрате»:
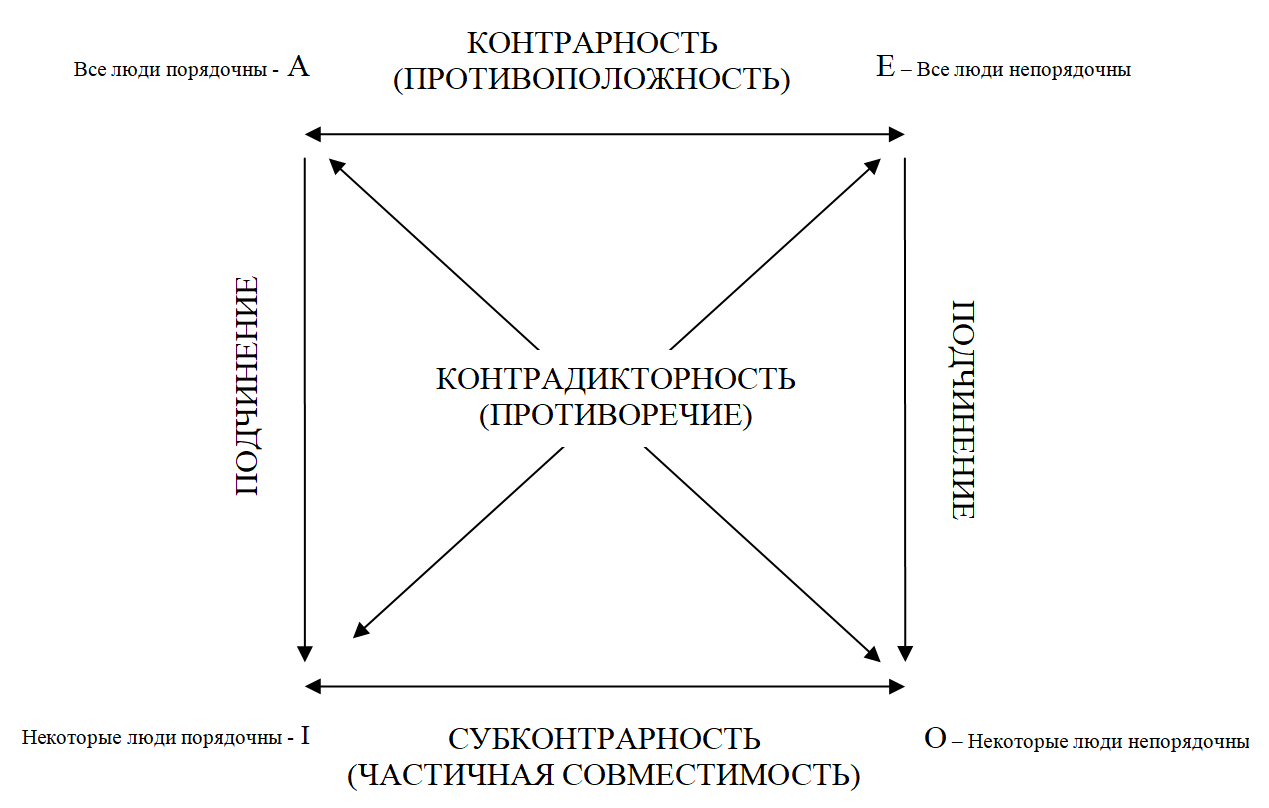
Для нас наиболее интересными являются отношения противоречия (контрадикторности) и противоположности (контрарности). Эту разницу студент должен чётко понимать.
Противоположные суждения не могут быть одновременно истинными, но могут быть одновременно ложными. Про такое отношение обычно говорят: суждения несовместимы по истинности, но могут быть совместимы по ложности. Примером таких суждений может быть:
Все люди философы — Все люди не являются философами
Противоречивые суждения несовместимы как по истинности, так и по ложности, т.е. не могут быть одновременно истинными и не могут быть одновременно ложными:
Все люди философы — Некоторые люди не являются философами
Именно по этому, противоречивые суждения являются полным отрицанием друг друга. Из выше изложенного становится понятной и процедура отрицания простого суждения. Чтобы осуществить отрицание суждения, нужно изменить его качественные и количественные характеристики на противоположные. Технически это осуществляется путём замены квантора на противоположный и отрицания на утверждение (утверждения на отрицание):
| суждение | ↔ | его отрицание |
| ¬(Все S суть P) | ↔ | Некоторые S не суть P |
| ¬(Все S не суть P) | ↔ | Некоторые S суть P |
| ¬(Некоторые S суть P) | ↔ | Все S не суть P |
| ¬(Некоторые S не P) | ↔ | Все S суть P |
Данная таблица читается и в обратном направлении:
| суждение | ↔ | его отрицание |
| Все S суть P | ↔ | ¬(Некоторые S не суть P) |
| Все S не суть P | ↔ | ¬(Некоторые S суть P) |
| Некоторые S суть P | ↔ | ¬(Все S не суть P) |
| Некоторые S не P | ↔ | ¬(Все S суть P) |
Помимо отрицания суждений есть и иные отношения между простыми суждениями. Важнейшими отношениями между простыми суждениями являются превращение и обращение.
Операцией превращение называется операция преобразования простого суждения из утвердительного в отрицательное и, наоборот, из отрицательного в утвердительное. Т.е. речь идет об изменении качества суждения.
Для правильной процедуры превращения необходимо запомнить два правила:
- Отрицание связки эквивалентно отрицанию свойства. Например, выражения «Все S не суть P» эквивалентно выражению «Все S суть не P».
- Двойное отрицание эквивалентно утверждению, а утверждение эквивалентно двойному отрицанию: A≡¬¬A и ¬¬A≡A.
Зная эти два правила, читатель может самостоятельно проводить операцию превращения. Ясно, выражение «Некоторые люди не являются философами» эквивалентно выражению «Некоторые люди являются не философами». А выражение «Некоторые люди являются философами» эквивалентно выражению «Некоторые люди не являются не философами».
При необходимости, читатель может запомнить эквивалентности, получаемые в результате превращений суждений:
| суждение | ↔ | его превращение |
| Все S суть P | ↔ | Ни одно S не суть не P |
| Все S не суть P | ↔ | Все S суть не P |
| Некоторые S суть P | ↔ | Некоторые S не суть не P |
| Некоторые S не суть P | ↔ | Некоторые S суть не P |
Важно
| Процедура превращения может быть крайне полезна в том случае, когда мы имеем, например, с частно-отрицательными суждениями, операции с которым ограничены. Превратив частно-отрицательное суждение в частно-утвердительное, дальнейшие выводы могут стать значительно богаче. |
Суть процедуры обращения заключается в том, мы меняем субъект и предикат суждения местами. Например, суждения вида «Некоторые люди млекопитающие» эквивалентно суждению «Некоторые млекопитающие – люди».
Сложность обращение заключается в том, что мы не вправе менять местами субъект и предикат автоматически. И здесь придется просто запомнить схемы обращения:
| суждение | ↔ | его обращение |
| Все S суть P | ↔ | Некоторые P суть S |
| Все S не суть P | ↔ | Все P не суть S |
| Некоторые S суть P | ↔ | Некоторые P суть S |
| Некоторые S не P | ≢ | не обращается! |
Дополнительная информация
_________________________________________________________________________________
Существует ещё две процедуры преобразования простых суждений — противопоставление предикату и противопоставление субъекту.
По сути, это не новые типы преобразований, поскольку противопоставление предикату представляет собой последовательное выполнение превращение, а затем обращение высказывания. Соответственно, противопоставление субъекту – это последовательное обращение и, затем, превращение высказывания.
Например, операцию противопоставления предикату можно представить следующим образом: 1. «Некоторые люди не являются философами» → 2. «Некоторые люди являются не философами» (превратили предыдущее суждение) → 3. «Некоторые не философы являются людьми» (обратили предыдущее суждение). Непосредственный переход от первого высказыванию к третьему называется противопоставлением предикату.
Операцию противопоставления субъекту можно представить аналогичным образом: 1. «Некоторые люди являются философами» → 2. «Некоторые философы являются людьми» (обратили предыдущее суждение) → 3. «Некоторые философы не являются нелюдями» (превратили предыдущее суждение). Непосредственный переход от первого высказыванию к третьему называется противопоставлением субъекту.
Зная правила обращения и превращения, читатель может самостоятельно проводить процедуры противопоставлений. Но, если читателю это делать лень, он может просто запомнить эквивалентности противопоставлений:
Противопоставление предикату:
| суждение | ↔ | противопоставление предикату |
| Все S суть P | ↔ | Ни одно не P не есть S |
| Все S не суть P | ↔ | Некоторые не P суть S |
| Некоторые S не суть P | ↔ | Некоторые не P суть S |
Противопоставление субъекту:
| суждение | ↔ | противопоставление субъекту |
| Все S суть P | ↔ | Ни одно P не суть не S |
| Все S не суть P | ↔ | Все P суть не S |
| Некоторые S суть P | ↔ | Некоторые P не суть не S |
